题目内容
7. 已知点P(1,3),Q(1,2).设过点P的动直线与抛物线y=x2交于A,B两点,直线AQ,BQ与该抛物线的另一交点分别为C,D.记直线AB,CD的斜率分
已知点P(1,3),Q(1,2).设过点P的动直线与抛物线y=x2交于A,B两点,直线AQ,BQ与该抛物线的另一交点分别为C,D.记直线AB,CD的斜率分别为k1,k2.
(Ⅰ)当k1=0时,求弦AB的长;
(Ⅱ)当k1≠2时,$\frac{{k}_{2}-2}{{k}_{1}-2}$是否为定值?若是,求出该定值.
分析 (Ⅰ)通过直线AB的方程:y=3,可得A、B坐标,计算即可;
(Ⅱ)通过设直线AB的方程:y-3=k1(x-1),联立直线AB与抛物线方程,利用韦达定理及A、Q、C三点共线,计算即得结论.
解答 解:(Ⅰ)∵点P(1,3),k1=0时,
∴直线AB的方程为:y=3,
∴A(-$\sqrt{3}$,3),B($\sqrt{3}$,3),
∴弦AB的长为$\sqrt{3}$-(-$\sqrt{3}$)=2$\sqrt{3}$;
(Ⅱ)∵直线AB的斜率为k1,
∴可设直线AB的方程为:y-3=k1(x-1),
设A(x1,${{x}_{1}}^{2}$),B(x2,${{x}_{2}}^{2}$),
联立直线AB与抛物线方程得$\left\{\begin{array}{l}{y={x}^{2}}\\{y={k}_{1}x-{k}_{1}+3}\end{array}\right.$,
消去y得x2-k1x+k1-3=0,
由韦达定理可得x1+x2=k1,x1x2=k1-3,
又设C(x3,${{x}_{3}}^{2}$),D(x4,${{x}_{4}}^{2}$),
则k2=$\frac{{{x}_{4}}^{2}-{{x}_{3}}^{2}}{{x}_{4}-{x}_{3}}$=x3+x4,
由于A、Q、C三点共线可得$\frac{{{x}_{3}}^{2}-{{x}_{1}}^{2}}{{x}_{3}-{x}_{1}}$=$\frac{{{x}_{1}}^{2}-2}{{x}_{1}-1}$,
即x3=1-$\frac{1}{{x}_{1}-1}$,
同理可得x4=1-$\frac{1}{{x}_{2}-1}$,
∴当k1≠2时,$\frac{{k}_{2}-2}{{k}_{1}-2}$=$\frac{{x}_{3}+{x}_{4}-2}{{x}_{1}+{x}_{2}-2}$
=-$\frac{1}{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1}$
=-$\frac{1}{({k}_{1}-3)-{k}_{1}+1}$
=$\frac{1}{2}$,
故当k1≠2时,$\frac{{k}_{2}-2}{{k}_{1}-2}$为定值$\frac{1}{2}$.
点评 本题是一道直线与抛物线的综合题,涉及到韦达定理等知识,考查分析问题、解决问题的能力,考查计算能力,注意解题方法的积累,属于中档题.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案| A. | (-∞,-1-$\sqrt{2}$] | B. | (-∞,${e}^{\frac{π}{2}}$-$\sqrt{2}$] | C. | (-∞,-1-$\sqrt{2}$${e}^{\frac{π}{2}}$] | D. | (-∞,(-1-$\sqrt{2}$)${e}^{\frac{π}{2}}$] |
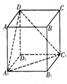
 如图,在正方体ABCD-A1B1C1D1中,O1为底面的中心,则O1A与上底面A1B1C1D1所成角的正切值是( )
如图,在正方体ABCD-A1B1C1D1中,O1为底面的中心,则O1A与上底面A1B1C1D1所成角的正切值是( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.
如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.