题目内容
(本题满分13分)
已知f(x)=ln(1+x2)+ax(a≤0)。
(1)讨论f(x)的单调性。
(2)证明:(1+ )(1+
)(1+ )…(1+
)…(1+ )<e (n∈N*,n≥2,其中无理数e=2.71828…)
)<e (n∈N*,n≥2,其中无理数e=2.71828…)
已知f(x)=ln(1+x2)+ax(a≤0)。
(1)讨论f(x)的单调性。
(2)证明:(1+
 )(1+
)(1+ )…(1+
)…(1+ )<e (n∈N*,n≥2,其中无理数e=2.71828…)
)<e (n∈N*,n≥2,其中无理数e=2.71828…)解:(理)(1)f′(x)=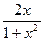 +a=
+a=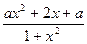 ………………………………1分
………………………………1分
(i)若a=0时,f′(x)=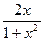 >0
>0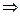 x>0,f′(x)<0
x>0,f′(x)<0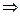 x<0
x<0
∴f(x)在(0,+∞)单调递增,在(-∞,0)单调递减。 …………………………3分
(ii)若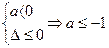 时,f′(x)≤0对x∈R恒成立。
时,f′(x)≤0对x∈R恒成立。
∴f(x)在R上单调递减。 ……………………………6分
(iii)若-1<a<0,由f′(x)>0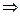
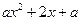 >0
>0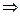
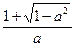 <x<
<x<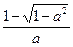
由f′(x)<0可得x>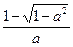 或x<
或x<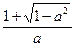
∴f(x)在[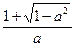 ,
,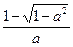 ]单调递增
]单调递增
在(-∞,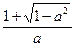 ],[
],[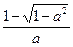
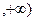 上单调递减。
上单调递减。
综上所述:若a≤-1时,f(x)在(-∞,+∞)上单调递减。………………………………7分
(2)由(1)当a=-1时,f(x)在(-∞,+∞)上单调递减。
当x∈(0,+∞)时f(x)<f(0)
∴ln(1+x2)-x<0 即ln(1+x2)<x
∴ln[(1+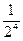 )(1+
)(1+ )……(1+
)……(1+ )]
)]
=ln[(1+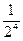 )(1+
)(1+ )+…ln(1+
)+…ln(1+ )<
)<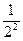 +
+ +…+
+…+
<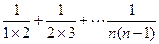 =1-
=1-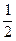 +
+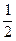 -
-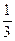 +…+
+…+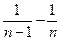 =1-
=1-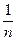 <1
<1
∴(1+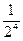 )(1+
)(1+ )……(1+
)……(1+ )<e …………………………………………13分
)<e …………………………………………13分
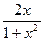 +a=
+a=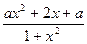 ………………………………1分
………………………………1分(i)若a=0时,f′(x)=
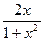 >0
>0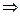 x>0,f′(x)<0
x>0,f′(x)<0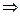 x<0
x<0∴f(x)在(0,+∞)单调递增,在(-∞,0)单调递减。 …………………………3分
(ii)若
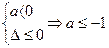 时,f′(x)≤0对x∈R恒成立。
时,f′(x)≤0对x∈R恒成立。∴f(x)在R上单调递减。 ……………………………6分
(iii)若-1<a<0,由f′(x)>0
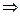
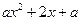 >0
>0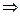
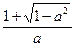 <x<
<x<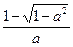
由f′(x)<0可得x>
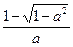 或x<
或x<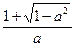
∴f(x)在[
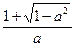 ,
,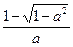 ]单调递增
]单调递增在(-∞,
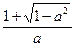 ],[
],[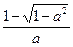
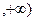 上单调递减。
上单调递减。综上所述:若a≤-1时,f(x)在(-∞,+∞)上单调递减。………………………………7分
(2)由(1)当a=-1时,f(x)在(-∞,+∞)上单调递减。
当x∈(0,+∞)时f(x)<f(0)
∴ln(1+x2)-x<0 即ln(1+x2)<x
∴ln[(1+
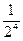 )(1+
)(1+ )……(1+
)……(1+ )]
)]=ln[(1+
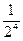 )(1+
)(1+ )+…ln(1+
)+…ln(1+ )<
)<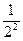 +
+ +…+
+…+
<
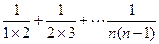 =1-
=1-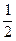 +
+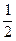 -
-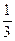 +…+
+…+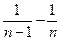 =1-
=1-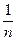 <1
<1∴(1+
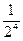 )(1+
)(1+ )……(1+
)……(1+ )<e …………………………………………13分
)<e …………………………………………13分
练习册系列答案
相关题目
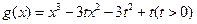
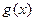 的单调区间;
的单调区间;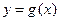 在点
在点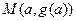 和
和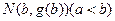 处的切线都与
处的切线都与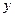 轴垂直,若方程
轴垂直,若方程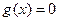 在区间
在区间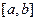 上有解,求实数
上有解,求实数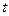 的取值范围。
的取值范围。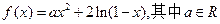 。
。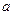 ,使得
,使得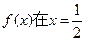 处取极值?试证明你的结论;
处取极值?试证明你的结论;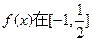 上是减函数,求实数
上是减函数,求实数
 且
且 ,求函数
,求函数 的极大值与极小值.
的极大值与极小值.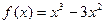 ,给出下列四个命题:①
,给出下列四个命题:①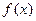 是增函数,无极值;②
是增函数,无极值;②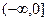 及
及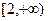 上是增函数;④
上是增函数;④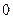 ,极小值
,极小值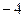 ;其中正确命题的个数为( )
;其中正确命题的个数为( )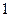

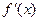 是
是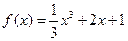 的导函数,则
的导函数,则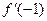 的值是 .
的值是 .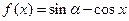 ,则
,则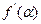 等于( )
等于( )



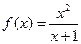 的导数。
的导数。