��Ŀ����
����Ŀ������4��23��������ʽ����ʵʩ��3+1+2���ĸ߿��·�������3����ָ�ؿ������ġ���ѧ����������ѧ�ƣ���1����ָ����������ʷ�б�ѡһ�ƣ���2����ָ�ڻ�ѧ��������Ρ������Ŀ�����ѡ���ƣ�Ϊ�˽���У��һѧ������������ʷ�е�ѡ����Ը�����������һ��ģ��ѡ��. ��֪��У��һ������������ʷѡ�Ƶ���1800��ѧ������������1000�ˣ�Ů��800��. ���ֲ�����ķ������г�ȡ��36��������ͳ��֪������17������ѡ������6��Ů��ѡ��ʷ��
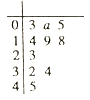
��I����������ȡ���������ݣ���д������е�������. ������![]() ͳ�����ж��ܷ���
ͳ�����ж��ܷ���![]() �İ�����Ϊѡ������������ʷ���Ա��йأ�
�İ�����Ϊѡ������������ʷ���Ա��йأ�
��II����������ѡ��ʷ��������ѡ4�ˣ���ѡ��4����������![]() �ˣ�Ů����
�ˣ�Ů����![]() �ˣ����������
�ˣ����������![]() �ķֲ��к���ѧ��������
�ķֲ��к���ѧ��������![]() �ļ��㹫ʽ���£�
�ļ��㹫ʽ���£�![]() ���ٽ�ֵ����
���ٽ�ֵ����
|
|
|
|
|
|
|
|
|
|
|
|
���𰸡���I��û��90%�İ�����Ϊѡ������������ʷ���Ա��йأ���II��������
��������
��I��������֪�����ֲ��������ȡ��36��������������![]() ��������16��Ů�������������г������������
��������16��Ů�������������г������������![]() ��ֵ�����ɵõ����ۣ�
��ֵ�����ɵõ����ۣ�
��II���ɣ�I��֪��������ѡ��ʷ����9��. ��������3�ˣ�Ů��6�ˣ����![]() ���ܵ�ȡֵ��
���ܵ�ȡֵ��![]() �����������Ӧ�ĸ��ʣ��г���������ķֲ��У����ù�ʽ���������
�����������Ӧ�ĸ��ʣ��г���������ķֲ��У����ù�ʽ���������
��I��������֪�����ֲ��������ȡ��36��������������![]() ��������16��Ů���������Ŀ���ݿɵ���������
��������16��Ů���������Ŀ���ݿɵ���������
���� | Ů�� | �ϼ� | |
ѡ���� | 17 | 3 | 20 |
ѡ��ʷ | 10 | 6 | 16 |
�ϼ� | 27 | 9 |
��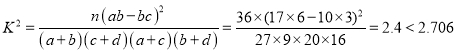
��![]() ��
��
����û��90%�İ�����Ϊѡ������������ʷ���Ա��й�.
��II���ɣ�I��֪��������ѡ��ʷ����9��. ��������3�ˣ�Ů��6�ˣ�
����![]() ���ܵ�ȡֵ��
���ܵ�ȡֵ��![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 2 | 0 |
|
|
|
|
|
|
|
����![]() ������
������![]() .
.

����Ŀ��ijӡˢ��Ϊ���о������鼮�ijɱ�![]() ����λ��Ԫ����ӡˢ����
����λ��Ԫ����ӡˢ����![]() ����λ��ǧ�ᣩ֮��Ĺ�ϵ����ӡ��ij���鼮ʱ������ͳ�ƣ�������ݼ��±���
����λ��ǧ�ᣩ֮��Ĺ�ϵ����ӡ��ij���鼮ʱ������ͳ�ƣ�������ݼ��±���
ӡˢ���� |
|
|
|
|
|
����ɱ� |
|
|
|
|
|
�����������ݣ�������Ա�ֱ�����ס������ֲ�ͬ�Ļع�ģ�ͣ��õ������ع鷽�̣����̼ף�![]() �������ң�
�������ң�![]() .
.
��1��Ϊ����������ģ�͵����Ч���������������.
������±�����������ȷ��![]() ����
����
ӡˢ���� |
|
|
|
|
| |
����ɱ� |
|
|
|
|
| |
ģ�ͼ� | ����ֵ |
|
|
| ||
�в� |
|
|
| |||
ģ���� | ����ֵ |
|
|
| ||
�в� |
|
|
| |||
�ڷֱ����ģ�ͼ���ģ���ҵIJв�ƽ���ͣ���ͨ���Ƚϣ��ж��ĸ�ģ�����Ч������.
��2����������֮���ܵ����������һ�ӭ�����ñ�ȫ������������ӡˢ���������ж���ӡˢ�������г����飬��������Ϊ![]() ǧ�ᣬ��ӡˢ����ÿ��
ǧ�ᣬ��ӡˢ����ÿ��![]() Ԫ�ļ۸��鼮���۸������̣���ӡˢ������ӡˢ
Ԫ�ļ۸��鼮���۸������̣���ӡˢ������ӡˢ![]() ǧ���õ���������1�������Ч���Ϻõ�ģ�ͼ���ӡˢ������ijɱ���.
ǧ���õ���������1�������Ч���Ϻõ�ģ�ͼ���ӡˢ������ijɱ���.