题目内容
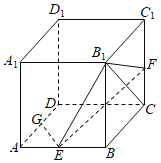
【题目】定义函数![]() ,其中x为自变量,a为常数.
,其中x为自变量,a为常数.
(1)若当x∈[0,2]时,函数fa(x)的最小值为﹣1,求a的值;
(2)设全集U=R,集合A={x|f3(x)≥0},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠![]() 中,求a的取值范围.
中,求a的取值范围.
【答案】(1)3;(2)![]()
【解析】
(1)设t=2x,换元后,变为二次函数,确定新元取值范围为![]() ,按对称轴与区间
,按对称轴与区间![]() 的关系求函数的最小值,从而可求得
的关系求函数的最小值,从而可求得![]() ;
;
(2)先求出集合UA,化简方程由题意fa(x)+fa(2﹣x)=f2(2),题意说明![]() (a+1)(
(a+1)(![]() )+2a﹣6=0在(0,log23)内有解,换元设t
)+2a﹣6=0在(0,log23)内有解,换元设t![]() ,由指数函数及对勾函数性质得t∈[4,5),问题可以转化为方程
,由指数函数及对勾函数性质得t∈[4,5),问题可以转化为方程![]() 在t∈[4,5)上有解,只要求得
在t∈[4,5)上有解,只要求得![]() ,t∈[4,5)的值域即可,这又可由函数单调性得出.
,t∈[4,5)的值域即可,这又可由函数单调性得出.
(1)令t=2x,∵x∈[0,2],∴t∈[1,4],
设φ(t)=t2﹣(a+1)t+a,t∈[1,4],
1°当![]() ,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
2°当![]() ,即
,即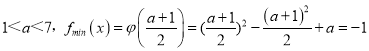 ,
,
解得a=3或a=﹣1,∵1<a<7,∴a=3;
3°当![]() ,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
解得![]() ,但与a≥7矛盾,故舍去,
,但与a≥7矛盾,故舍去,
综上所述,a的值为3.
(2)UA={x|4x﹣42x+3<0}={x|0<x<log23},
B={x|4x﹣(a+1)2x+a+42﹣x﹣(a+1)22﹣x+a=6}![]() .
.
由已知(UA)∩B≠![]() 即
即![]() (a+1)(
(a+1)(![]() )+2a﹣6=0在(0,log23)内有解,
)+2a﹣6=0在(0,log23)内有解,
令t![]() ,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
也等价于方程![]() 在t∈[4,5)上有解,
在t∈[4,5)上有解,
∵![]() 在t∈[4,5)上单调递增,
在t∈[4,5)上单调递增,
∴h(t)∈[﹣1,2),
故所求a的取值范围是[﹣1,2).

练习册系列答案
相关题目