Question

2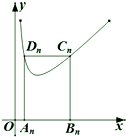．如图，矩形A_nB_nC_nD_n的一边A_nB_n在x轴上，另外两个顶点C_n，D_n在函数f（x）=x+$\frac{1}{x}$（x＞0）的图象上．若点B_n的坐为（n，0）（n≥2，n∈N₊），记矩形A_nB_nC_nD_n的周长为a_n，则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=（　　）

• A． 9×2¹³
• B． 9×2¹⁴-32
• C． 9×2¹⁴-24
• D． 9×2¹³+24

Answer 1

分析 根据题意，求出矩形A_nB_nC_nD_n的一组相邻边长，计算出它的周长，
再求a₂•${2}^{\frac{{a}_{2}}{4}}$+a₃•${2}^{\frac{{a}_{3}}{4}}$+a₄•${2}^{\frac{{a}_{4}}{4}}$+…+a₁₀•${2}^{\frac{{a}_{10}}{4}}$的值即可．

解答 解：由题意，∵C_n，D_n在函数f（x）=x+$\frac{1}{x}$（x＞0）的图象上，
且点B_n的坐标为（n，0）（n≥2，n∈N₊），
∴C_n的纵坐标为n+$\frac{1}{n}$，D_n的横坐标为$\frac{1}{n}$，
∴矩形A_nB_nC_nD_n的一条边长为n+$\frac{1}{n}$，另一条边长为n-$\frac{1}{n}$，
∴矩形A_nB_nC_nD_n的周长为a_n=2（n+$\frac{1}{n}$+n-$\frac{1}{n}$）=4n；
∴a₂•${2}^{\frac{{a}_{2}}{4}}$+a₃•${2}^{\frac{{a}_{3}}{4}}$+a₄•${2}^{\frac{{a}_{4}}{4}}$+…+a₁₀•${2}^{\frac{{a}_{10}}{4}}$=4×2•2²+4×3•2³+4×4•2⁴+…+4×10•2¹⁰
=4×（2•2²+3•2³+4•2⁴+…+10•2¹⁰）；
设S=2•2²+3•2³+4•2⁴+…+10•2¹⁰，
则2S=2•2³+3•2⁴+4•2⁵+…+10•2¹¹，
∴S=2S-S=-2•2²-2³-2⁴-2⁵-…-2¹⁰+10•2¹¹
=-2²-（2²+2³+2⁴+..+2¹⁰）+10•2¹¹
=-2²-$\frac{{2}^{2}（1{-2}^{9}）}{1-2}$+10•2¹¹
=-2²+2²-2¹¹+10•2¹¹
=9•2¹¹；
∴${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=4×9•2¹¹=9×2¹³．
故选：A．

点评 本题考查了利用错位相减法求数列的前n项和的问题，也考查了学生分析解决问题的能力，其中求矩形A_nB_nC_nD_n的周长是解题的关键．