题目内容
7．已知e为自然对数的底数，若曲线y=xex在点（1，e）处的切线方程为y=2ex-e．分析 求出函数的导数，求得切线的斜率，由点斜式方程即可得到所求切线的方程．
解答 解：y=xex的导数为y′=（1+x）ex，
在点（1，e）处的切线斜率为k=2e，
即有在点（1，e）处的切线方程为y-e=2e（x-1），
即为y=2ex-e．
故答案为：y=2ex-e．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义和直线方程的求法，属于基础题．
练习册系列答案
期末集结号系列答案
相关题目
18．下列命题中正确的个数为（ ）
①纯虚数集相对复数集的补集是虚数集；
②复数z是实数的充要条件是z=$\overline{z}$；
③复数z是纯虚数的充要条件是z+$\overline{z}$=0；
④i+1的共轭复数是i-1．
①纯虚数集相对复数集的补集是虚数集；
②复数z是实数的充要条件是z=$\overline{z}$；
③复数z是纯虚数的充要条件是z+$\overline{z}$=0；
④i+1的共轭复数是i-1．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
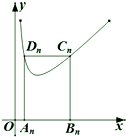如图，矩形AnBnCnDn的一边AnBn在x轴上，另外两个顶点Cn，Dn在函数f（x）=x+$\frac{1}{x}$（x＞0）的图象上．若点Bn的坐为（n，0）（n≥2，n∈N+），记矩形AnBnCnDn的周长为an，则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=（ ）
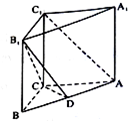在直三棱柱ABC-A1B1C1中，已知AB=5，AC=4，BC=3，AA1=4，点D在棱AB上．