题目内容
【题目】已知
是定义在R上的偶函数且以2为周期，则“为
上的增函数”是“为
上的减函数”的
A. 充分而不必要的条件B. 必要而不充分的条件
C. 充要条件D. 既不充分也不必要的条件
【答案】C
【解析】
由题意，可由函数的性质得出
在
上是减函数，再由函数的周期性即可得出为
上的减函数，由此证明充分性，再由为上的减函数结合周期性即可得出为上是减函数，再由函数是偶函数即可得出为
上的增函数，由此证明必要性，即可得出正确选项
解：
是定义在R上的偶函数，
若为上的增函数，则为上是减函数，
又是定义在R上的以2为周期的函数，且与相差两个周期，两区间上的单调性一致，所以可以得出为上的减函数，故充分性成立．
若为上的减函数，同样由函数周期性可得出为上是减函数，再由函数是偶函数可得出为上的增函数，故必要性成立．
综上，“为上的增函数”是“为上的减函数”的充要条件．
故选：C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】火把节是彝族、白族、纳西族、基诺族、拉祜族等民族的古老传统节日，有着深厚的民俗文化内涵，被称为“东方的狂欢节”凉山州旅游局为了解民众对火把节知识的知晓情况，对西昌市区 A,B 两小区的部分居民开展了问卷调查，他们得分(满分100分)数据，统计结果如下：
A小区 | ||||
得分范围/分 |
|
|
|
|
频率 |
|
|
|
|
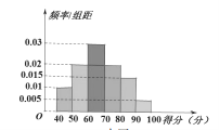
B小区
（1）以每组数据的中点值作为该组数据的代表，求B小区的平均分；
（2）若A小区得分在
内的人数为
人，B小区得分在内的人数为
人，求在 A，B 两小区中所有参加问卷调查的居民中得分不低于
分的频率；
