��Ŀ����
����Ŀ��������Բ C : ![]()
![]() ����Բ����ԭ�㣬�뾶Ϊ
����Բ����ԭ�㣬�뾶Ϊ![]() ��Բ����Բ C ��������Բ��.����Բ C ��һ������Ϊ F1(
��Բ����Բ C ��������Բ��.����Բ C ��һ������Ϊ F1(![]() , 0) ��������ϵ�һ���˵㵽 F1 �ľ���Ϊ
, 0) ��������ϵ�һ���˵㵽 F1 �ľ���Ϊ![]()
��1������Բ C �ķ��̼���������Բ�����̣�
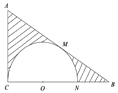
��2������б�� 45����ֱ�� l ����Բ C ֻ��һ�������㣬������Բ C �İ���Բ�ཻ�� M .N ���㣬���� MN �ĵij���
��3���� P ����Բ C �İ���Բ��һ�����㣬���� P ��ֱ�� l1��l2��ʹ�� l1��l2����Բ C ��ֻ��һ�������㣬�ж�l1��l2��λ�ù�ϵ����˵������.
���𰸡���1����Բ���̣�![]() ������Բ���̣� x2 y2 1 ����2�� 2
������Բ���̣� x2 y2 1 ����2�� 2![]() ����3����ֱ����б�ʳ˻�Ϊ 1 ����б�ʴ������
����3����ֱ����б�ʳ˻�Ϊ 1 ����б�ʴ������
��������
��1��ֱ������ԲC��һ������Ϊ![]() ��������ϵ�һ���˵㵽F1�ľ���Ϊ
��������ϵ�һ���˵㵽F1�ľ���Ϊ![]() ���������������ԲC�ķ��̼��䡰����Բ�����̣�
���������������ԲC�ķ��̼��䡰����Բ�����̣�
��2���Ȱ�ֱ�߷�������Բ�������������ö�Ӧ���б�ʽΪ0������������ֱ�߷����Լ�Բ�ĵ�ֱ�ߵľ��룻��������MN�ij���
��3���ȶ�ֱ��l1��l2��б���Ƿ���ڷ�����������ۣ�Ȼ���ÿһ������е�ֱ��l1��l2����ԲC��ֻ��һ�������������⼴��֤��l1��l2������б�ʴ���ʱ��������ֱ�߷��̣���ֱ������Բ��������������б��Ϊ��Ӧ���̵ĸ����жϽ��ۣ���
�⣺��1����Ϊ![]() ������b��1
������b��1
������Բ�ķ���Ϊ![]() ��
��
����Բ�ķ���Ϊx2+y2��4��
��2����ֱ��l�ķ���y��x+b����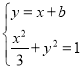 ��4x2+6bx+3b2��3��0
��4x2+6bx+3b2��3��0
�ɡ�����6b��2��16��3b2��3����0��b2��4
Բ�ĵ�ֱ��l�ľ���Ϊ![]()
����![]()
��3������l1��l2����һ����б��ʱ��������l1��б�ʣ�
��Ϊl1����Բֻ��һ�������㣬���䷽��Ϊ![]() ��
��![]() ��
��
��l1����Ϊ![]() ʱ����ʱl1�����Բ���ڵ�
ʱ����ʱl1�����Բ���ڵ�![]() ��
��
��ʱ������![]() ����
����![]() ������Բֻ��һ���������ֱ����y��1����y����1����
������Բֻ��һ���������ֱ����y��1����y����1����
��l2Ϊy��1����y����1������Ȼֱ��l1��l2��ֱ��
ͬ����֤l1����Ϊ![]() ʱ��ֱ��l1��l2��ֱ��
ʱ��ֱ��l1��l2��ֱ��
����l1��l2����б��ʱ�����P��x0��y0��������x02+
�辭����P��x0��y0��������Բֻ��һ���������ֱ��Ϊy��k��x��x0��+y0��
��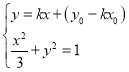 ����ȥy�õ�x2+3��kx+��y0��kx0����2��3��0��
����ȥy�õ�x2+3��kx+��y0��kx0����2��3��0��
����1+3k2��x2+6k��y0��kx0��x+3��y0��kx0��2��3��0��
����[6k��y0��kx0��]2��4��1+3k2��[3��y0��kx0��2��3]��0��
��������õ�����3��x02��k2+2x0y0k+1��y02��0��
��Ϊx02+y02��4�������У�3��x02��k2+2x0y0k+��x02��3����0��
��l1��l2��б�ʷֱ�Ϊk1��k2����Ϊl1��l2����Բ��ֻ��һ�������㣬
����k1��k2���㷽�̣�3��x02��k2+2x0y0k+��x02��3����0��
���k1k2����1����l1��l2��ֱ��