题目内容
8.已知等差数列{an}的前n项和Sn满足S3=6,S5=$\frac{25}{2}$.(Ⅰ)求{an}的通项公式;
(II)求数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和.
分析 (I)通过S3=6,S5=$\frac{25}{2}$,计算即得结论;
(Ⅱ)通过(Ⅰ)知$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n+2}{{2}^{n+1}}$,利用错位相减法计算Tn-$\frac{1}{2}$Tn,计算即得结论.
解答 解:(I)设等差数列{an}的公差为d,则Sn=$n{a}_{1}+\frac{n(n-1)}{2}d$,
∵S3=6,S5=$\frac{25}{2}$,
∴$\left\{\begin{array}{l}{3{a}_{1}+3d=6}\\{5{a}_{1}+10d=\frac{25}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=\frac{3}{2}}\\{d=\frac{1}{2}}\end{array}\right.$,
∴{an}的通项公式为:an=$\frac{1}{2}$n+1;
(Ⅱ)设求数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和为Tn,
由(Ⅰ)知$\frac{{a}_{n}}{{2}^{n}}$=$\frac{n+2}{{2}^{n+1}}$,
则:Tn=3•$\frac{1}{{2}^{2}}$+4•$\frac{1}{{2}^{3}}$+5•$\frac{1}{{2}^{4}}$+…+(n+1)•$\frac{1}{{2}^{n}}$+(n+2)•$\frac{1}{{2}^{n+1}}$,
∴$\frac{1}{2}$Tn=3•$\frac{1}{{2}^{3}}$+4•$\frac{1}{{2}^{4}}$+…+(n+1)•$\frac{1}{{2}^{n+1}}$+(n+2)•$\frac{1}{{2}^{n+2}}$,
两式相减得:$\frac{1}{2}$Tn=$\frac{3}{4}$+($\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n+1}}$)-(n+2)•$\frac{1}{{2}^{n+2}}$=$\frac{3}{4}$+$\frac{1}{4}$(1-$\frac{1}{{2}^{n-1}}$)-$\frac{n+2}{{2}^{n+2}}$,
∴Tn=2-$\frac{n+4}{{2}^{n+1}}$.
点评 本题考查求数列的通项及前n项和,考查运算求解能力,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
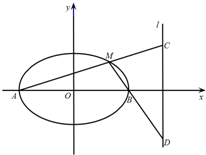 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.