题目内容
16.如图,等腰三角形OAB(O为坐标原点)的顶点A,B的坐标分别为(6,0),(3,3),AB与直线y=$\frac{1}{2}$x交于点C,在△OAB中任取一点P,则点P落在△OBC中的概率( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 求出直线AB的方程以及C的坐标,根据几何概型的概率公式求出对应的面积进行求解即可.
解答 解:∵顶点A,B的坐标分别为(6,0),(3,3),
∴AB的方程为$\frac{y-0}{3-0}=\frac{x-6}{3-6}$,
即y=-x+6,
由$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{1}{2}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,即C(4,2)
则△OAC的面积S=$\frac{1}{2}×6×2=6$,
△OAB的面积S=$\frac{1}{2}×6×3=9$,
则三角形OBC的面积S=9-6=3,
故点P落在三角形OBC中的概率为$\frac{3}{9}=\frac{1}{3}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,根据条件求出C的坐标以及阴影部分的面积是解决本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7.设a∈[0,4],则使方程x2+ax+1=0有解的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
5.房山区某高中为了推进新课程改革,满足学生全面发展的需求,决定从高一年级开始,在每周的周一、周三、周五的格外活动期间同时开设信息技术、美术素描和音乐欣赏辅导讲座,每位同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
(1)求音乐欣赏辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
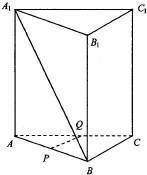 如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.
如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.