题目内容
17.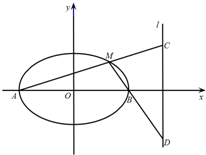 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.(Ⅰ)求椭圆G的标准方程;
(Ⅱ)若|CD|=4,求点M的坐标;
(Ⅲ)记△MAB和△MCD的面积分别为S1和S2,若λ=$\frac{{S}_{1}}{{S}_{2}}$,求实数λ的取值范围.
分析 (1)根据题意列式求得椭圆方程,
(2)直线AM的斜率k显然存在,且k>0,故可设直线AM的方程为y=k(x+2),由$\left\{\begin{array}{l}{x=4}\\{y=k(x+2)}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=6k}\end{array}\right.$利用条件求得.
(3)根据面积公式列式利用均值不等式求得.
解答 解:(1)由e=$\frac{{\sqrt{3}}}{2}$,得$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{3}{4}$①,又(c,$\frac{1}{2}$)在椭圆上,代入得$\frac{{c}^{2}}{{a}^{2}}+\frac{\frac{1}{4}}{{b}^{2}}=1$②
由①②解得a2=4,b2=1,
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$
(2)直线AM的斜率k显然存在,且k>0,故可设直线AM的方程为y=k(x+2)
由$\left\{\begin{array}{l}{x=4}\\{y=k(x+2)}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=6k}\end{array}\right.$∴C(4,6k)
由$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y并整理得,(1+4k2)x2+16k2x+16k2-4=0
设M(x0,y0),则(-2)x0=$\frac{16{k}^{2}-4}{1+4{k}^{2}}$,∴${x}_{0}=\frac{2-8{k}^{2}}{1+4{k}^{2}}$,从而${y}_{0}=\frac{4k}{1+4{k}^{2}}$,
即M($\frac{2-8{k}^{2}}{1+4{k}^{2}},\frac{4k}{1+4{k}^{2}}$),又B(2,0)
故直线BM的方程为$y=-\frac{1}{4k}(x-2)$
由$\left\{\begin{array}{l}{x=4}\\{y=-\frac{1}{4k}(x-2)}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=-\frac{1}{2k}}\end{array}\right.$,∴$D(4,-\frac{1}{2k})$
∴$|CD|=|6k+\frac{1}{2k}|=6k+\frac{1}{2k}(k>0)$
由|CD|=4,得6k+$\frac{1}{2k}$=4,解得k=$\frac{1}{2}$,或k=$\frac{1}{6}$
从而求得M(0,1)或M($\frac{8}{5},\frac{3}{5}$).
(3)由(1)得$M(\frac{2-8{k}^{2}}{1+4{k}^{2}},\frac{4k}{1+4{k}^{2}})$.
∴${S}_{1}=\frac{1}{2}|AB||{y}_{M}|=\frac{1}{2}×4×|\frac{4k}{1+4{k}^{2}}|=\frac{8k}{1+4{k}^{2}}$
${S}_{2}=\frac{1}{2}|CD||4-{x}_{M}|=\frac{1}{2}×|6k+\frac{1}{2k}|×$$|4-\frac{2-8{k}^{2}}{1+4{k}^{2}}|=\frac{(1+12{k}^{2})^{2}}{2k(1+4{k}^{2})}$
假设存在实数λ,使得S1=λS2,则
$λ=\frac{{S}_{1}}{{S}_{2}}=\frac{16{k}^{2}}{(1+12{k}^{2})^{2}}=\frac{16{k}^{2}}{1+24{k}^{2}+144{k}^{4}}$=$\frac{16}{144{k}^{2}+\frac{1}{{k}^{2}}+24}≤\frac{16}{2\sqrt{144{k}^{2}•\frac{1}{{k}^{2}}}+24}=\frac{1}{3}$
当且仅当$144{k}^{2}=\frac{1}{{k}^{2}}$,即$k=\frac{\sqrt{3}}{6}$时,等号成立.
又∵λ>0,∴$0≤λ≤\frac{1}{3}$
故存在$λ∈(0,\frac{1}{3}]$,使得S1=λS2
点评 本题主要考查了直线与圆锥曲线的综合性问题,在高考中属于常考题型.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
 用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )| A. | $\sqrt{3}+1$ | B. | 1 | C. | $\sqrt{2}+1$ | D. | 3 |
| A. | -2,8 | B. | 2,-8 | C. | 64,-16 | D. | 16,-64 |