题目内容
【题目】如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
注：年份代码1﹣7分别对应年份2008﹣2014．
（1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；
（2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
附注：
参考数据： 
=9.32， 
=40.17， 
=0.55， 
≈2.646．
参考公式： 
，
回归方程 
中斜率和截距的最小二乘估计公式分别为：
， 
．
【答案】
（1）
解：由折线图看出，y与t之间存在较强的正相关关系，理由如下：
∵ 
= 
≈ 
≈ 
≈0.996，
∵0.996＞0.75，
故y与t之间存在较强的正相关关系；
（2）
解： 
= 
≈ 
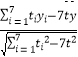≈0.10，
≈1.331﹣0.10×4≈0.93，
∴y关于t的回归方程 
=0.103+0.93，
2016年对应的t值为9，
故 =0.10×9+0.93=1.83，
预测2016年我国生活垃圾无害化处理量为1.83亿吨．
【解析】（1）由折线图看出，y与t之间存在较强的正相关关系，将已知数据代入相关系数方程，可得答案；（2）根据已知中的数据，求出回归系数，可得回归方程，2016年对应的t值为9，代入可预测2016年我国生活垃圾无害化处理量．本题考查的知识点是线性回归方程，回归分析，计算量比较大，计算时要细心．
【题目】某商场经销某商品，根据以往资料统计，顾客采用的付款期数X的分布列为
X | 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．Y表示经销一件该商品的利润．
(1)求事件：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率P(A)；
(2)求Y的分布列及E(Y)．
