Question

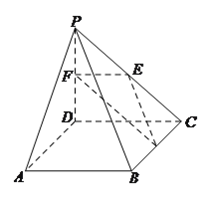
【题目】如图所示，在三棱柱ABC－A1B1C1中，△ABC与△A1B1C1都为正三角形且AA1⊥面ABC，F、F1分别是AC，A1C1的中点．

求证：(1)平面AB1F1∥平面C1BF；

(2)平面AB1F1⊥平面ACC1A1.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：（1）要证，只需证、，只需证、，而四边形、四边形皆为平行四边形，所以得证；（2）要证，只需证，只需证、，其中易知可得，△A1B1C1为正三角形可得，从而得证．

试题解析：（1）连接，在三棱柱中，由为棱的中点，所以，四边形是平行四边形,所以,又,则.又在矩形中可得,且, ，则,而， 且，所以．

（2）因为， ，所以，又因为△A1B1C1为正三角形， 的中点，所以，又，所以，因为，所以．