题目内容
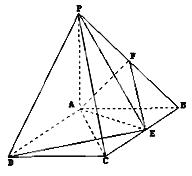
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
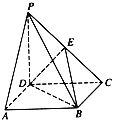
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() (如图2).
(如图2).

(1)证明:平面![]() 平面
平面![]() ;
;
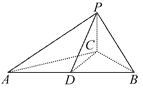
(2)试在棱![]() 上确定一点
上确定一点![]() ,使截面
,使截面![]() 把几何体分成的两部分
把几何体分成的两部分![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:I)依题意知:CD⊥AD,即可根据面面垂直的性质定理可得:所以DC⊥平面PAD,再根据面面垂直的判定定理可得:平面PAD⊥平面PCD.
(II)根据(I)同理可得:PA⊥平面ABCD,可得平面PAB⊥平面ABCD.在AB上取一点N,MN⊥平面ABCD,设MN=h,再分别计算出VPDCMA与VMABC的数值,并且结合题意可得![]() ,所以M为PB的中点.
,所以M为PB的中点.
试题解析:
(1)因为PDCB为等腰梯形,PB=3,DC=1,PA=1,则PA⊥AD,CD⊥AD.
又因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD面ABCD,故CD⊥面PAD.
又因为CD面PCD,所以平面PAD⊥平面PCD.
(2)所求的点M即为线段PB的中点.
证明如下:
设三棱锥M-ACB的高为h1,四棱锥P-ABCD的高为h2,
当M为线段PB的中点时,![]()
所以, ![]() 所以截面AMC把几何体分成的两部分VP-DCMA∶VM-ACB=2∶1.
所以截面AMC把几何体分成的两部分VP-DCMA∶VM-ACB=2∶1.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目