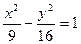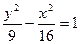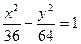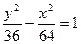题目内容
(本题满分12分)
双曲线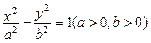 的左、右焦点分别为
的左、右焦点分别为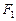 、
、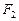 ,
, 为坐标原点,点
为坐标原点,点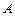 在双曲线的右支上,点
在双曲线的右支上,点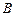 在双曲线左准线上,
在双曲线左准线上,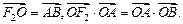
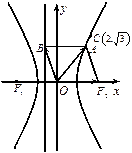
(Ⅰ)求双曲线的离心率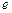 ;
;
(Ⅱ)若此双曲线过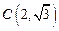 ,求双曲线的方程;
,求双曲线的方程;
(Ⅲ)在(Ⅱ)的条件下,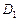 、
、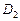 分别是双曲线的虚轴端点(
分别是双曲线的虚轴端点(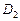 在
在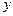 轴正半轴上),过
轴正半轴上),过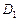 的直线
的直线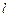 交双曲线
交双曲线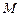 、
、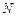 ,
,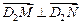 ,求直线
,求直线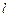 的方程
的方程
双曲线
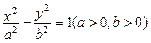 的左、右焦点分别为
的左、右焦点分别为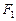 、
、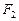 ,
,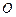 为坐标原点,点
为坐标原点,点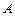 在双曲线的右支上,点
在双曲线的右支上,点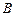 在双曲线左准线上,
在双曲线左准线上,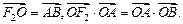
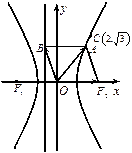
(Ⅰ)求双曲线的离心率
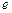 ;
;(Ⅱ)若此双曲线过
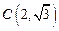 ,求双曲线的方程;
,求双曲线的方程;(Ⅲ)在(Ⅱ)的条件下,
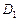 、
、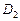 分别是双曲线的虚轴端点(
分别是双曲线的虚轴端点(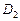 在
在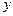 轴正半轴上),过
轴正半轴上),过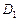 的直线
的直线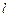 交双曲线
交双曲线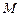 、
、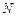 ,
,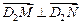 ,求直线
,求直线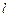 的方程
的方程(Ⅰ)2
(Ⅱ)
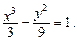
(Ⅲ)
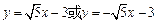
解:(Ⅰ)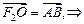 四边形
四边形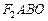 是平行四边形,
是平行四边形,
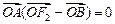 即
即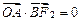 ,
,
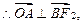 ∴平行四边形
∴平行四边形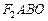 是菱形.
是菱形.
如图,则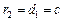 ,
,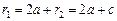 ,
,
由双曲线定义得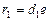
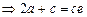
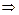
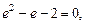
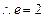 (
(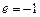 舍去) …………3分
舍去) …………3分
(Ⅱ)由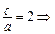
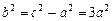 ,
,
双曲线方程为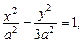
把点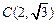 代入有得
代入有得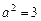 ,
,
∴双曲线方程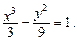 ………6分
………6分
(Ⅲ)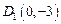 ,
,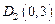 ,设
,设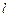 的方程为
的方程为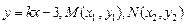
则由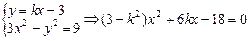 ,
,
因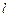 与与双曲线有两个交点,
与与双曲线有两个交点,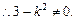
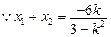 ,
,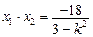 ,
,
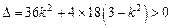 …………8分
…………8分
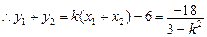 ,
,
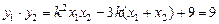
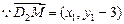 ,
, ,
,
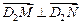
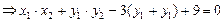
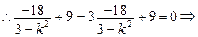
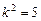 ,
,
满足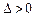 ,
,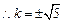 …………10分
…………10分
故所求直线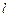 方程为
方程为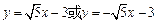 …………12分
…………12分
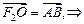 四边形
四边形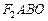 是平行四边形,
是平行四边形,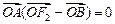 即
即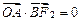 ,
,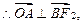 ∴平行四边形
∴平行四边形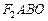 是菱形.
是菱形.如图,则
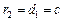 ,
,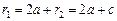 ,
,由双曲线定义得
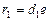
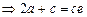
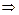
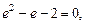
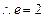 (
(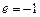 舍去) …………3分
舍去) …………3分(Ⅱ)由
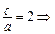
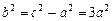 ,
,双曲线方程为
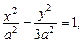
把点
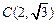 代入有得
代入有得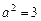 ,
,∴双曲线方程
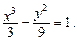 ………6分
………6分(Ⅲ)
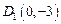 ,
,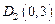 ,设
,设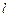 的方程为
的方程为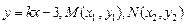
则由
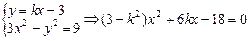 ,
,因
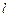 与与双曲线有两个交点,
与与双曲线有两个交点,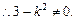
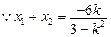 ,
,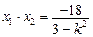 ,
,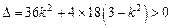 …………8分
…………8分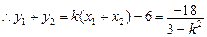 ,
,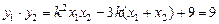
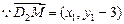 ,
, ,
,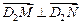
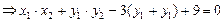
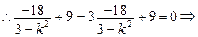
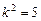 ,
,满足
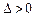 ,
,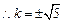 …………10分
…………10分故所求直线
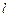 方程为
方程为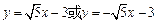 …………12分
…………12分
练习册系列答案
相关题目
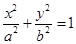 (a>b>0)的离心率e=
(a>b>0)的离心率e=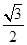 ,则双曲线
,则双曲线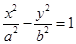 离心率为
离心率为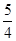
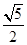
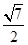
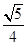
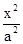 -
-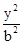 =1(a>0,b>0)的一条渐近线方程为y=x,则有
=1(a>0,b>0)的一条渐近线方程为y=x,则有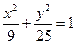 共焦点,他们的离心率之和为
共焦点,他们的离心率之和为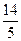 ,求双曲线的标准方程
,求双曲线的标准方程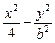 =1(b∈N)的两个焦点
=1(b∈N)的两个焦点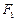 、
、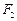 ,
,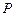 为双曲线上一点,
为双曲线上一点,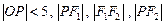 成等比数列,则
成等比数列,则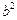 =_____
=_____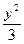 =1,过P(2,1)点作一直线交双曲线于A、B两点,并使P为AB的中点,则直线AB的斜率为______
=1,过P(2,1)点作一直线交双曲线于A、B两点,并使P为AB的中点,则直线AB的斜率为______ 的右焦点是抛物线的焦点,则抛物线的标准方程是 ▲ .
的右焦点是抛物线的焦点,则抛物线的标准方程是 ▲ .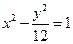 上的一点,
上的一点,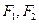 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若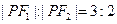 ,则
,则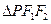 的面积为___________.
的面积为___________.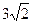 , 4)的双曲线的标准方程是( )
, 4)的双曲线的标准方程是( )