题目内容
已知,在△ABC中,AB=2AC,AD是∠A的平分线,交BC于点D,且AD=k•AC.
(1)求k的取值范围;
(2)若△ABC的面积为1,求BC最短时k的值.
(1)求k的取值范围;
(2)若△ABC的面积为1,求BC最短时k的值.
考点:三角形的面积公式
专题:解三角形
分析:(1)如图所示,在△ABC中,AD是∠A的平分线,AB=2AC,利用角平分线的性质定理可得:
=
=
,∠1=∠2.令AC=a,DC=b,AD=c,则AB=2a,BD=2b.在△ABD与△ACD中,分别利用余弦定理可得:BD2=AB2+AD2-2AB•AD•cos∠1,DC2=AC2+AD2-2AC•ADcos∠2,化简整理即可得出.
(2)由于△ABC的面积为1,可得
•2a•a•sinA=1,可得sinA=
.求BC最短时k的值,只考虑A为锐角或直角时即可.可得cosA=
=
.
在△ABC中,由余弦定理可得:BC2=4a2+a2-4a2•cosA=5a2-4
,令a2=t>0,f(t)=5t-4
,利用导数研究其单调性极值与最值即可得出.
| BD |
| DC |
| AB |
| AC |
| 2 |
| 1 |
(2)由于△ABC的面积为1,可得
| 1 |
| 2 |
| 1 |
| a2 |
| 1-sin2A |
| ||
| a2 |
在△ABC中,由余弦定理可得:BC2=4a2+a2-4a2•cosA=5a2-4
| a4-1 |
| t2-1 |
解答:
解:(1)如图所示,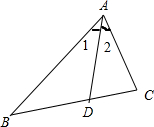
∵在△ABC中,AD是∠A的平分线,AB=2AC,
∴
=
=
,∠1=∠2.
令AC=a,DC=b,AD=c,则AB=2a,BD=2b.
在△ABD与△ACD中,分别利用余弦定理可得:
BD2=AB2+AD2-2AB•AD•cos∠1,
DC2=AC2+AD2-2AC•ADcos∠2,
∴4b2=4a2+c2-4accos∠1,b2=a2+c2-2ac•cos∠2,
化为3c2-4accos∠1=0,又c=ka,
∴k=
cos∠1,
∵∠1∈(0,
),∴cos∠1∈(0,1).
∴k∈(0,
).
(2)∵△ABC的面积为1,
∴
•2a•a•sinA=1,可得sinA=
.
∵求BC最短时k的值,∴只考虑A为锐角或直角时即可.
∴cosA=
=
.
在△ABC中,由余弦定理可得:BC2=4a2+a2-4a2•cosA=5a2-4
,
令a2=t>0,f(t)=5t-4
,
则f′(t)=5-
,
令f′(t)=0,解得t=
.
当t>
时,f′(t)>0,此时函数f(t)单调递增;当0<t<
时,f′(t)<0,此时函数f(t)单调递减.
∴当t=
时,函数f(t)取得最小值,即BC2=5×
-4
=3.
此时cosA=
=2cos2∠1-1,解得cos∠1=
.
∴k=
cos∠1=
×
=
.

∵在△ABC中,AD是∠A的平分线,AB=2AC,
∴
| BD |
| DC |
| AB |
| AC |
| 2 |
| 1 |
令AC=a,DC=b,AD=c,则AB=2a,BD=2b.
在△ABD与△ACD中,分别利用余弦定理可得:
BD2=AB2+AD2-2AB•AD•cos∠1,
DC2=AC2+AD2-2AC•ADcos∠2,
∴4b2=4a2+c2-4accos∠1,b2=a2+c2-2ac•cos∠2,
化为3c2-4accos∠1=0,又c=ka,
∴k=
| 4 |
| 3 |
∵∠1∈(0,
| π |
| 2 |
∴k∈(0,
| 4 |
| 3 |
(2)∵△ABC的面积为1,
∴
| 1 |
| 2 |
| 1 |
| a2 |
∵求BC最短时k的值,∴只考虑A为锐角或直角时即可.
∴cosA=
| 1-sin2A |
| ||
| a2 |
在△ABC中,由余弦定理可得:BC2=4a2+a2-4a2•cosA=5a2-4
| a4-1 |
令a2=t>0,f(t)=5t-4
| t2-1 |
则f′(t)=5-
| 4t | ||
|
令f′(t)=0,解得t=
| 5 |
| 3 |
当t>
| 5 |
| 3 |
| 5 |
| 3 |
∴当t=
| 5 |
| 3 |
| 5 |
| 3 |
(
|
此时cosA=
| 4 |
| 5 |
3
| ||
| 10 |
∴k=
| 4 |
| 3 |
| 4 |
| 3 |
3
| ||
| 10 |
2
| ||
| 5 |
点评:本题考查了三角形内角平分线的性质定理、余弦定理、三角形的面积计算公式、同角三角函数基本关系式,考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
复数
的共轭复数等于( )
| 1 |
| (1+i)2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若实数x,y满足条件
,则目标函数z=x+2y的最小值是( )
|
| A、-2 | B、2 | C、4 | D、6 |
 如图,在四棱锥V-ABCD中,四边形ABCD的对角线AC,BD相交于点O,已知底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图,在四棱锥V-ABCD中,四边形ABCD的对角线AC,BD相交于点O,已知底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为