题目内容
【题目】设二阶矩阵A＝
.
（1） 求A－1；
（2） 若曲线C在矩阵A对应的变换作用下得到曲线C′：6x2－y2＝1，求曲线C的方程．
【答案】（1） A－1＝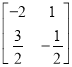
；（2） 8y2－3x2＝1.
【解析】
（1）根据逆矩阵公式直接得到；
（2）设曲线C上任意一点P（x，y）在矩阵A对应的变换作用下得到点P′（x′，y′），根据矩阵变换可得
，将（x′，y′）代入曲线C′：6x2－y2＝1，即可得到结果.
（1） 根据逆矩阵公式，可得A－1＝.
（2） 设曲线C上任意一点P（x，y）在矩阵A对应的变换作用下得到点P′（x′，y′），
则
＝
＝
，
所以
因为（x′，y′）在曲线C′上，所以6x′2－y′2＝1，代入得6（x＋2y）2－（3x＋4y）2＝1，化简得8y2－3x2＝1，
所以曲线C的方程为8y2－3x2＝1.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
