题目内容
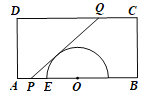
【题目】已知动圆M与直线
相切，且与圆N：
外切
（1）求动圆圆心M的轨迹C的方程；
（2）点O为坐标原点，过曲线C外且不在y轴上的点P作曲线C的两条切线，切点分别记为A，B，当直线
与
的斜率之积为
时，求证：直线过定点.
【答案】（1）
；（2）见解析
【解析】
（1）直接利用直线与圆的位置关系式，圆和圆的位置关系式的应用求出结果．
（2）利用直线与曲线的相切和一元二次方程根和系数关系式的应用求出结果．
（1）设动圆圆心M（x，y），
由于圆M与直线y=-1相切，且与圆N：
外切．
利用圆心到直线的距离和圆的半径和圆心距之间的关系式，
可知C的轨迹方程为：
（2）设直线
：
，
，
，
因为，
，所以两条切线的斜率分别为
，
，
则直线
的方程是
，
直线
的方程是
.
两个方程联立得P点坐标为
，
，
，由
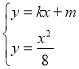联立得：
，
故直线过定点
.
练习册系列答案
阅读快车系列答案
相关题目
