题目内容
【题目】已知椭圆![]() 的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为
的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为![]() .
.
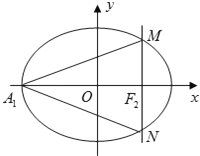
(Ⅰ)求椭圆的离心率;
(Ⅱ)若△A1MN的外接圆在M处的切线与椭圆相交所得弦长为![]() ,求椭圆方程.
,求椭圆方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)由已知得点![]() 坐标,由
坐标,由![]() ,得
,得 ,解得
,解得![]() ;(Ⅱ)由(Ⅰ)得
;(Ⅱ)由(Ⅰ)得![]() ,
,![]() ,又外心
,又外心![]() 在
在![]() 轴上,设为
轴上,设为![]() ,则由
,则由![]() ,解得
,解得![]()
![]() ,故
,故![]() ,所以经过点
,所以经过点![]() 的切线方程为
的切线方程为![]() ,联立椭圆方程,消去
,联立椭圆方程,消去![]() ,得
,得![]() ,则由弦长公式可得弦长为
,则由弦长公式可得弦长为![]() ,解得
,解得![]() ,故所求方程为
,故所求方程为![]() .
.
试题解析:(Ⅰ)由题意![]()
因为A1(﹣a,0),所以![]()
将b2=a2﹣c2代入上式并整理得![]() (或a=2c)
(或a=2c)
所以![]()
(Ⅱ)由(Ⅰ)得a=2c,![]() (或
(或![]() )
)
所以A1(﹣2c,0)![]() ,外接圆圆心设为P(x0,0)
,外接圆圆心设为P(x0,0)
由|PA1|=|PM|,得![]()
解得:![]()
所以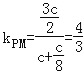
所以△A1MN外接圆在M处切线斜率为![]() ,设该切线与椭圆另一交点为C
,设该切线与椭圆另一交点为C
则切线MC方程为![]() ,即
,即![]()
与椭圆方程3x2+4y2=12c2联立得7x2﹣18cx+11c2=0
解得![]()
由弦长公式![]() 得
得![]()
解得c=1
所以椭圆方程为![]()

练习册系列答案
相关题目