题目内容
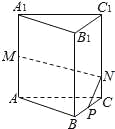
【题目】如图，在正三棱柱
中，AB=3，
=4，M为的中点，P是BC边上的一点，且由点P沿棱柱侧面经过棱
到M点的最短路线长为
，设这条最短路线与的交点为N，求
（1）该三棱柱的侧面展开图的对角线长.
（2）PC和NC的长
（3）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）
【答案】（1）
（2）PC=2，NC=
（3）
【解析】
（1）由展开图为矩形，用勾股定理求对角线长．
（2）在侧面展开图中三角形MAP是直角三角形，可以求出线段AP的长度，进而可以求出PC的长度，再由相似比可以求得CN的长度．
（3）补形，找出两面的交线，由三垂线定理作出二面角的平面角，二面角易求．
解：(1)正三棱柱
的侧面展开图是一个长为9,宽为4的矩形
故其对角线长为
；
(2)如图,将侧面
绕棱
旋转120使其与侧面
在同一平面上,点P运动到点
的位置,连接
,则就是由点P沿棱柱侧面经过棱到点M的最短路线
设
，则
，在
中，由勾股定理得x=2,
，
，
；
(3)如图,连接
，则就是平面NMP与平面ABC的交线,作NH⊥于H,又⊥平面ABC,连接CH,由三垂线定理得,CH⊥，
∴∠NHC就是平面NMP与平面ABC所成二面角的平面角(锐角)，
在
中, 
，
，
在
中, 
，
故平面NMP与平面ABC所成二面角(锐角)的大小为，
【题目】一般来说，一个人脚掌越长，他的身高就越高，现对10名成年人的脚掌
与身高
进行测量，得到数据（单位：cm）作为样本如表所示：
脚掌长（ | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高（ | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
（1）在上表数据中，以“脚掌长”为横坐标，“身高”为纵坐标，作出散点图后，发现散点在一条直线附近，试求“身高”与“脚掌长”之间的线性回归方程
；
（2）若某人的脚掌长为26.5cm，试估计此人的身高；
（3）在样本中，从身高180cm以上的4人中随机抽取2人进行进一步的分析，求所抽取的2人中至少有1人身高在190cm以上的概率.
（参考数据：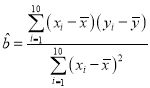
，
，
，
，
）
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况，在本市的所有中学生中随机抽取了120名学生进行调查，现将日均自学时间小于1小时的学生称为“自学不足”者
根据调查结果统计后，得到如下
列联表，已知在调查对象中随机抽取1人，为“自学不足”的概率为
．
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
请完成上面的列联表；
根据列联表的数据，能否有
的把握认为“自学不足”与“配有智能手机”有关？
附表及公式: 
，其中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
