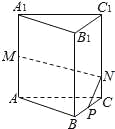
题目内容
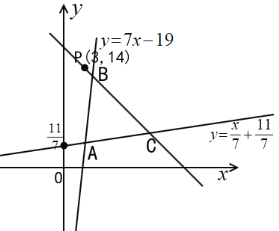
【题目】已知等腰三角形△ABC的两腰AB和AC所在直线的方程分别为
和
是底边BC上一点,求:
(1)底边BC所在直线的方程；
(2)△ABC的面积.
【答案】（1）
或
；（2）54或96
【解析】
（1）设出底边BC所在直线的方程，利用直线到直线的成角公式列方程求解；
（2）求出点
到直线BC的距离，以及线段BC的长，利用三角形面积公式求解即可.
设底边BC所在直线的方程为
，即
，
则直线AB到直线BC所成的角等于直线BC到直线AC所成的角，于是有
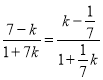，解得
或
，
所以底边BC所在直线的方程为
或
，
即或；
（2）联立方程
，解得，
当底边BC所在直线的方程为时，
点到直线BC：的距离为
，
联立方程
，解得
，
联立方程
，解得
，
，
；
当底边BC所在直线的方程为时，
点到直线BC：的距离为
，
联立方程
，解得
，
联立方程
，解得
，
，
；
综上：△ABC的面积为54或96.
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
【题目】在万众创新的大经济背景下，某成都青年面包店推出一款新面包，每个面包的成本价为
元，售价为
元，该款面包当天只出一炉（一炉至少
个，至多
个），当天如果没有售完，剩余的面包以每个
元的价格处理掉，为了确定这一炉面包的个数，该店记录了这款新面包最近天的日需求量（单位：个），整理得下表：
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）根据表中数据可知，频数
与日需求量
（单位：个）线性相关，求关于
的线性回归方程；
（2）以天记录的各日需求量的频率代替各日需求量的概率，若该店这款新面包出炉的个数为
，记当日这款新面包获得的总利润为
（单位：元）.求的分布列及其数学期望.
相关公式：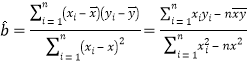
，
