题目内容
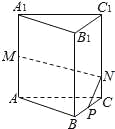
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]()

(1)证明:![]() 平面
平面![]() ;
;
(2)如果二面角![]() 的正切值为2,求
的正切值为2,求![]() 的值.
的值.
【答案】(1)祥见解析;(2)a=2.
【解析】
试题(1)由PO⊥平面ABCD,得PO⊥AD,由∠ADC=45°,AD=AC,得AD⊥AC,从而证明AD⊥平面PAC.(2)法一,先利用三垂线定理作出二面角M-AC-D的平面角:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角.然后在直角三角形MHG中,可用a表示出的正切值,从而由已知即可求出a的值;法二,以OA为x轴,OP为y轴,O为坐标原点建立空间直角坐标系,利用空间向量知亦可求.
试题解析: (1)证明:由题意,∠ADC=45o,AD=AC =1,故∠DAC=90o
即DA⊥AC.又因为 PO⊥平面ABCD,
所以,DA⊥PO,DA⊥平面PAC 4分
(2)法一:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角. 8分
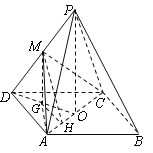
因为GH⊥AO,且G为DO中点,所以![]() ,而
,而![]() ,故
,故![]() ,PO="2MG=2." 12分
,PO="2MG=2." 12分
法二:建立如图所示的空间直角坐标系O-xyz,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
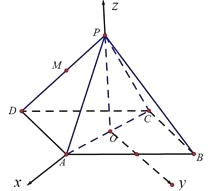
设平面MAC的法向量为![]() ,
,![]() ,
,![]() ,则
,则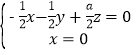 ,所以
,所以![]() 的一个取值为
的一个取值为
![]() 10分
10分
平面ACD的法向量为![]() .
.
设二面角的平面角为![]() ,
,
因为![]() ,所以
,所以![]()
a=2 12分

【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: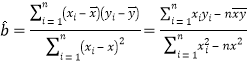 ,
,![]()