题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() , O为DE的中点,
, O为DE的中点,![]() .F为
.F为![]() 的中点,平面
的中点,平面![]() 平面BCED.
平面BCED.
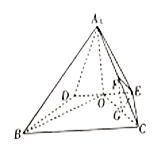
(1)求证:平面 ![]() 平面
平面![]() .
.
(2)线段OC上是否存在点G,使得![]() 平面EFG?说明理由。
平面EFG?说明理由。
【答案】(1)证明见解析 (2)不存在,理由见解析
【解析】
(1)题中已知垂直等关系易得![]() 平面
平面![]() ,因此关键是证明
,因此关键是证明![]() ,则可得线面垂直,从而有面面垂直,而
,则可得线面垂直,从而有面面垂直,而![]() 可在等腰梯形
可在等腰梯形![]() 中通过计算由勾股定理逆定理得证;
中通过计算由勾股定理逆定理得证;
(2)假设存在点![]() 满足题意,则可证得
满足题意,则可证得![]() ,
,![]() 是
是![]() 中点,从而有
中点,从而有![]() ,这与已知矛盾,从而得假设错误,点不存在.
,这与已知矛盾,从而得假设错误,点不存在.
解:(1)因为![]() .所以
.所以![]() ,又O为DE的中点,
,又O为DE的中点,
所以![]() .
.
因为平面![]() 平面BCED,且
平面BCED,且![]() 平面
平面![]() ,
,
所以![]() 平面BCED.所以
平面BCED.所以![]() .
.
由于四边形BCED是一个上底为2.下底为4,腰长为![]() 的等腰梯形,易求得
的等腰梯形,易求得![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
所以![]() 平面
平面![]() .所以平面
.所以平面 ![]() 平面
平面![]() .
.
(2)线段OC上不存在点G,使得![]() 平面FFG.
平面FFG.
理由如下:
假设线段OC上存在点G,使得![]() 平面EFG,
平面EFG,
连接GE,GF.则必有![]() .且
.且![]() .
.
在![]() 中,由F为
中,由F为![]() 的中点,
的中点,![]() ,得G为OC的中点.
,得G为OC的中点.
在![]() 中,因为
中,因为![]() .所以
.所以![]() .这显然与
.这显然与![]() ,
,![]() 矛盾.
矛盾.
所以线段OC上不存在点G,使得![]() 平面EFG.
平面EFG.

练习册系列答案
相关题目