题目内容
2.已知圆O:x2+y2=4,动直线l1:x-ky+2k=0和l2:kx+y-4k=0(k∈R).(1)试判断直线l1和圆O的位置关系,并说明理由;
(2)已知直线l2与圆O相交,直线l1被圆O截得的弦的中点为M,求动点M的轨迹方程.
分析 (1)动直线l1经过定点A(0,2),而点A在圆O上,由此可得直线l1和圆O的位置关系.
(2)由l2和圆O相交,可得弦心距小于半径,求得k的范围.设直线l1被圆O截得的弦的中点为M(x,y),则线段OM和直线l1垂直,它们的斜率之积等于-1,
即 $\frac{y}{x}$•$\frac{1}{k}$=-1,化简可得结果.
解答 解:(1)动直线l1:x-ky+2k=0,即 x-k(y-2)=0,经过定点A(0,2),
而点A在圆O:x2+y2=4上,故直线l1:x-ky+2k=0和圆O至少有一个交点,故直线l1和圆O相交或相切.
(2)由l2:kx+y-4k=0和圆O:x2+y2=4相交,可得弦心距$\frac{|4k|}{\sqrt{{k}^{2}+1}}$<2,求得k2<$\frac{1}{3}$,即-$\frac{\sqrt{3}}{3}$<k<$\frac{\sqrt{3}}{3}$,
设直线l1被圆O截得的弦的中点为M(x,y),则线段OM和直线l1垂直,∴$\frac{y}{x}$•$\frac{1}{k}$=-1,
即 y=-kx(-$\frac{\sqrt{3}}{3}$<k<$\frac{\sqrt{3}}{3}$ ),表示一条线段.
点评 本题主要考查直线经过定点问题,直线和圆的位置关系,圆的弦的性质,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)=$\frac{1}{1-x}$,g(x)=lnx,x0是函数h(x)=f(x)+g(x)的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | h(x1)<0,h(x2)<0 | B. | h(x1)>0,h(x2)>0 | C. | h(x1)>0,h(x2)<0 | D. | h(x1)<0,h(x2)>0 |
14.若复数z满足(z-3)(2-i)=5(i为虚数单位),则z为( )
| A. | 2-i | B. | 2+i | C. | 5-i | D. | 5+i |
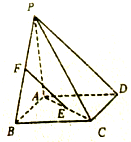 如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.
如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°. 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).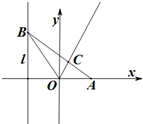 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C. 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).