题目内容
10.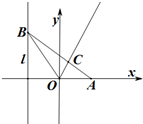 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.(1)求点C的轨迹方程;
(2)若E(-2,0),F(2,0),G(-1,$\frac{1}{2}$),(1)中轨迹上是否存在一点Q,直线EQ,FQ与y轴交点分别为M,N,使得∠MGN是直角?如果存在,求点Q坐标;如果不存在,请说明理由.
分析 (1)设B(-1,b),求得直线OA和OB的方程,设C(x,y),则0≤x<1,C到直线OA和OB的距离相等.运用点到直线的距离公式,化简整理,即可得到轨迹方程;
(2)设点Q(x0,y0),求得直线EQ,FQ的方程,令x=0,求得M,N的坐标,假设∠MGN是直角,由垂直的条件:斜率之积为-1,推理判断可得.
解答 解:(1)设B(-1,b),直线OA和OB的方程分别为
y=0与y=-bx,直线AB的方程为:y=-$\frac{b}{2}$(x-1).
设C(x,y),则0≤x<1,C到直线OA和OB的距离相等.
∴$\frac{|y+bx|}{\sqrt{1+{b}^{2}}}$=|y|,①
又C在直线AB上,所以:y=-$\frac{b}{2}$(x-1),即b=$\frac{2y}{1-x}$,代入①得:
y2[1+$\frac{4{y}^{2}}{(x-1)^{2}}$]=(y+$\frac{2xy}{1-x}$)2,整理得:y2(y2-x)=0,
若y≠0,则y2=x(0<x<1);
若y=0,则b=0,∠AOB=π,点C为(0,0),满足上式,
综上,点C的轨迹方程为:y2=x(0≤x<1);
(2)设点Q(x0,y0),则直线EQ,FQ的方程分别为:
y=$\frac{{y}_{0}}{{x}_{0}+2}$(x+2),y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),
令x=0得y=$\frac{2{y}_{0}}{2+{x}_{0}}$,y=$\frac{-2{y}_{0}}{{x}_{0}-2}$,∴M(0,$\frac{2{y}_{0}}{2+{x}_{0}}$),N(0,$\frac{-2{y}_{0}}{{x}_{0}-2}$),
∴直线MG,NG的斜率分别为:k1=$\frac{2{y}_{0}}{2+{x}_{0}}$-$\frac{1}{2}$,k2=$\frac{-2{y}_{0}}{{x}_{0}-2}$-$\frac{1}{2}$,
若∠MGN是直角,则k1k2=($\frac{2{y}_{0}}{2+{x}_{0}}$-$\frac{1}{2}$)($\frac{-2{y}_{0}}{{x}_{0}-2}$-$\frac{1}{2}$)=-1,
整理得-4y02+4y0=5-$\frac{5}{4}$x02②,
∵y02=x0(0≤x0<1),∴-1<y0<1,
∴-4y02+4y0=-(2y0-1)2+1≤1,5-$\frac{5}{4}$x02>5-$\frac{5}{4}$=$\frac{15}{4}$>1,
∴②式无解,从而∠MGN不可能是直角,
(1)中轨迹上不存在点Q满足题设.
点评 本题考查轨迹方程的求法,考查抛物线的方程的运用,直线方程和直线的斜率的运用,考查推理和运算求解能力,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | (-$\frac{70}{3}$,+∞) | B. | (16,+∞) | C. | (-$\frac{70}{3}$,16) | D. | (-$\frac{70}{4}$,-16) |
| A. | 0 | B. | -2 | C. | 2 | D. | 4 |
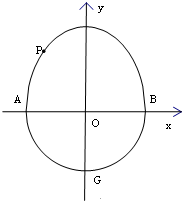 半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$.
半椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(y≥0)$和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0,如图所示,曲线C交x轴于A,B两点,交y轴负半轴于点G.椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$的离心率为$\frac{{\sqrt{2}}}{2}$,F是它的一个焦点,点P是曲线C位于x轴上方的任意一点,且△PFG的周长是$2\sqrt{2}+2$.