题目内容
用数学归纳法证明: …
… >
> (n∈N*,且n>2)时,第二步由
(n∈N*,且n>2)时,第二步由
“n=k到n=k+1”的证明,不等式左端增添代数式是( )
 …
… >
> (n∈N*,且n>2)时,第二步由
(n∈N*,且n>2)时,第二步由“n=k到n=k+1”的证明,不等式左端增添代数式是( )
A. | B. + + - -  |
C. + + | D. - -  |
B
略

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
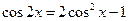 (
(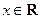 )的两边求导,得:
)的两边求导,得: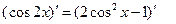 ,
,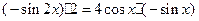 ,化简得等式:
,化简得等式: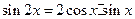 。
。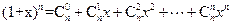 (
(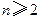 ),证明:
),证明: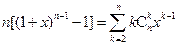 。
。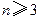 ,求证:
,求证: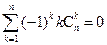 ; (ii)
; (ii)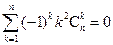 ; (iii)
; (iii)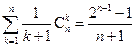 。
。 ,且
,且 求证:
求证: 中至少有一个是负数。
中至少有一个是负数。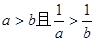 ,则
,则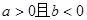 .
.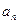 }的前n项和为
}的前n项和为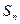 ,并且满足
,并且满足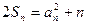 ,
,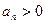 (n∈N*).
(n∈N*).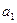 ,
,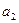 ,
,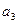 ;
;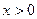 ,
,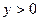 ,且
,且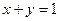 ,证明:
,证明: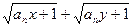 ≤
≤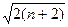 .
.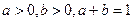 求证:
求证: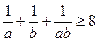 (用两种方法证明).
(用两种方法证明).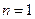 时,有
时,有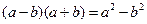
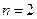 时,有
时,有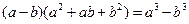
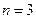 时,有
时,有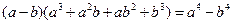
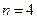 时,有
时,有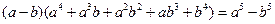
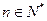 时,你能得到的结论是: .
时,你能得到的结论是: . ,则
,则

 则正确的结论是( )
则正确的结论是( )


 大小不定
大小不定