题目内容
用反证法证明“如果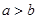 ,那么
,那么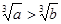 ”时,假设的内容应是
”时,假设的内容应是
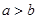 ,那么
,那么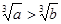 ”时,假设的内容应是
”时,假设的内容应是A.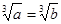 | B.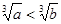 | C.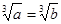 且 且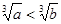 | D.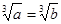 或 或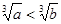 |
D
专题:阅读型.
分析:分析:反证法是假设命题的结论不成立,即结论的反面成立,所以只要考虑
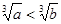
的反面是什么即可.
解答:解:∵
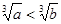 的反面是
的反面是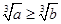 ,
,即
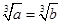 或
或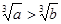 .
.故选D.
点评:本题主要考查了不等式证明中的反证法,属于基础题.

练习册系列答案
相关题目
题目内容
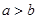 ,那么
,那么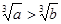 ”时,假设的内容应是
”时,假设的内容应是A.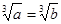 | B.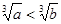 | C.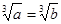 且 且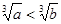 | D.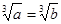 或 或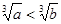 |
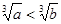
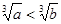 的反面是
的反面是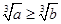 ,
,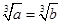 或
或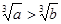 .
.