题目内容
【题目】
已知函数![]() ,
,![]() 。
。
(1)若函数![]() 在
在![]() 处的切线与函数
处的切线与函数![]() 在
在![]() 处的切线互相平行,求实数
处的切线互相平行,求实数![]() 的值;
的值;
(2)设函数![]() 。
。
(ⅰ)当实数![]() 时,试判断函数
时,试判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(ⅱ)如果![]() 是
是![]() 的两个零点,
的两个零点,![]() 为函数
为函数![]() 的导函数,证明:
的导函数,证明:![]() 。
。
【答案】(1)![]() ;(2)(i)函数
;(2)(i)函数![]() 在
在![]() 上单调递减.(ii)见解析。
上单调递减.(ii)见解析。
【解析】
试题分析:(1)分别求函数![]() 的导数得
的导数得![]() ,
,![]() ,由
,由![]() 求出
求出![]() 即可;(2)(i)由
即可;(2)(i)由 ![]() 及
及![]() 可得
可得![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递减;(ii)由
上单调递减;(ii)由![]() 是
是![]() 的两个零点,可得
的两个零点,可得![]() ,
,![]() ,从而有
,从而有![]() ,即
,即 ,所以
,所以![]()
 ,构造函数
,构造函数![]() ,讨论其单调性可得
,讨论其单调性可得![]() ,又
,又![]() ,从而证得结论成立。
,从而证得结论成立。
试题解析:(1)由![]() ,
,![]() 得,在
得,在![]() 处切线互相平行时,切线斜率相等,于是
处切线互相平行时,切线斜率相等,于是![]() ,
,![]() 。
。
(2)(1)![]()
易知![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]()
当![]() 时,
时,![]() 在
在![]() 上恒成立。
上恒成立。
∴当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减。
上单调递减。
(2)因为![]() 是
是![]() 的两个零点,故
的两个零点,故![]() ①
①
![]() ②,由②-①得:
②,由②-①得:![]()
解得
因为![]() ,
,![]()
将 代入得
代入得
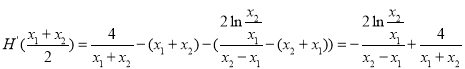
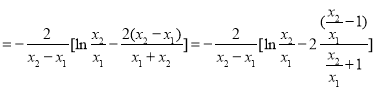
设![]() ,构造
,构造![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 单调增且
单调增且![]() ,∴
,∴![]() ,又
,又![]()
∴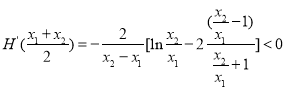 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在英语中不同字母出现的频率彼此不同且相差很大,但同一个字母的使用频率相当稳定,有人统计了40多万个单词中5个元音字母的使用频率,结果如下表所示:
元音字母 | A | E | I | O | U |
频率 | 7.88% | 12.68% | 7.07% | 7.76% | 2.80% |
(1)从一本英文(小说类)书里随机选一页,统计在这一页里元音字母出现的频率;
(2)将你统计得出的频率与上表中的频率进行比较,结果是否比较接近?你认为存在差异的原因是什么.
【题目】某种产品的质量以其指标值来衡量,其指标值越大表明质量越好,且指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分别估计用![]() 配方,
配方,![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(Ⅱ)已知用![]() 配方生产的一件产品的利润
配方生产的一件产品的利润![]() (单位:元)与其指标值
(单位:元)与其指标值![]() 的关系式为
的关系式为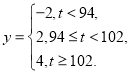
估计用![]() 配方生产的一件产品的利润大于0的概率,并求用
配方生产的一件产品的利润大于0的概率,并求用![]() 配方生产的上述产品平均每件的利润。
配方生产的上述产品平均每件的利润。