题目内容
【题目】某种产品的质量以其指标值来衡量,其指标值越大表明质量越好,且指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分别估计用![]() 配方,
配方,![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(Ⅱ)已知用![]() 配方生产的一件产品的利润
配方生产的一件产品的利润![]() (单位:元)与其指标值
(单位:元)与其指标值![]() 的关系式为
的关系式为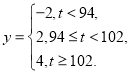
估计用![]() 配方生产的一件产品的利润大于0的概率,并求用
配方生产的一件产品的利润大于0的概率,并求用![]() 配方生产的上述产品平均每件的利润。
配方生产的上述产品平均每件的利润。
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() 。
。
【解析】
试题分析:(Ⅰ)借助题设条件运用频率分布表提供的数据分析求解;(Ⅱ)借助题设条件运用加权平均数公式求解.
试题解析:
(Ⅰ)由实验结果知,用![]() 配方生产的产品的优质的频率的估计值为
配方生产的产品的优质的频率的估计值为![]() ,
,
∴用![]() 配方生产的产品的优质品率的估计值为0.3。
配方生产的产品的优质品率的估计值为0.3。
由试验结果知,用![]() 配方生产的产品中优质品的频率为
配方生产的产品中优质品的频率为![]() ,
,
∴用![]() 配方生产的产品的优质品率的估计值为0.42。
配方生产的产品的优质品率的估计值为0.42。
(Ⅱ)解:由条件知,用![]() 配方生产的一件产品的利润大于0当且仅当其质量指标
配方生产的一件产品的利润大于0当且仅当其质量指标![]() ,
,
由试验结果知,指标值![]() 的频率为0.96,
的频率为0.96,
所以用![]() 配方生产的一件产品的利润大于0的概率估计值为0.96。
配方生产的一件产品的利润大于0的概率估计值为0.96。
用![]() 配方生产的产品平均每件的利润为
配方生产的产品平均每件的利润为![]() 元。
元。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目