题目内容
【题目】为探索课堂教学改革,惠来县某中学数学老师用传统教学和“导学案”两种教学方式,在甲、乙两个平行班进行教学实验.为了解教学效果,期末考试后,分别从两个班级各随机抽取20名学生的成绩进行统计,得到如下茎叶图.记成绩不低于70分者为“成绩优良”.
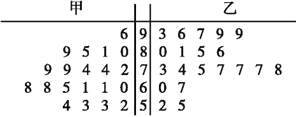
(Ⅰ)分析甲、乙两班的样本成绩,大致判断哪种教学方式的教学效果更佳,并说明理由;
(Ⅱ)由以上统计数据完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
参考公式:![]() ,其中
,其中![]() 是样本容量.
是样本容量.
独立性检验临界值表:

【答案】(Ⅰ)见解析(Ⅱ)能
【解析】
(Ⅰ)根据茎叶图中数据的特征,可知数据越集中,成绩越稳定,也即是效果越好,进而可得出结果;
(Ⅱ)根据题意写出列联表,结合表中数据求出![]() 的观测值,结合临界值表,即可求出结果.
的观测值,结合临界值表,即可求出结果.
(Ⅰ)乙班(“导学案”教学方式)教学效果更佳.
理由1、乙班大多在70以上,甲班70分以下的明显更多;
理由2、甲班样本数学成绩的平均分为:70.2;乙班样本数学成绩前十的平均分为:79.05,高10%以上.
理由3、甲班样本数学成绩的中位数为![]() , 乙班样本成绩的中位数
, 乙班样本成绩的中位数![]() ,高10%以上.
,高10%以上.
(Ⅱ)列联表如下:
甲班 | 乙班 | 总计 | |
成绩优良 | 10 | 16 | 26 |
成绩不优良 | 10 | 4 | 14 |
总计 | 20 | 20 | 40 |
由上表可得![]() .
.
所以能在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
(Ⅰ) 从III型号汽车的回访客户中随机选取1人,则这个客户不满意的概率为________;
(Ⅱ) 从所有的客户中随机选取1个人,估计这个客户满意的概率;
(Ⅲ) 汽车公司拟改变投资策略,这将导致不同型号汽车的满意率发生变化.假设表格中只有两种型号汽车的满意率数据发生变化,那么哪种型号汽车的满意率增加0.1,哪种型号汽车的满意率减少0.1,使得获得满意的客户人数与样本中的客户总人数的比值达到最大?(只需写出结论)
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |

其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.