题目内容
【题目】如图,在正方体ABCD-ABCD中,平面![]() 垂直于对角线AC,且平面
垂直于对角线AC,且平面![]() 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
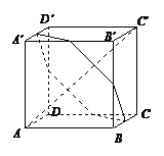
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
【答案】B
【解析】
将正方体切去两个正三棱锥![]() 和
和![]() ,得到一个几何体
,得到一个几何体![]() ,
,![]() 是以平行平面
是以平行平面![]() 和
和![]() 为上下底,每个侧面都是直角等腰三角形,截面多边形的每一条边分别与
为上下底,每个侧面都是直角等腰三角形,截面多边形的每一条边分别与![]() 的底面上的一条边平行,设正方体棱长为
的底面上的一条边平行,设正方体棱长为![]() ,
,![]() ,可求得六边形的周长为
,可求得六边形的周长为![]() 与
与![]() 无关,即周长为定值;当
无关,即周长为定值;当![]() 都在对应棱的中点时,
都在对应棱的中点时,![]() 是正六边形,计算可得面积
是正六边形,计算可得面积![]() ,当
,当![]() 无限趋近于
无限趋近于![]() 时,
时,![]() 的面积无限趋近于
的面积无限趋近于![]() ,从而可知
,从而可知![]() 的面积一定会发生变化。
的面积一定会发生变化。
设平面![]() 截得正方体的六个表面得到截面六边形为
截得正方体的六个表面得到截面六边形为![]() ,
,![]() 与正方体的棱的交点分别为
与正方体的棱的交点分别为![]() (如下图),
(如下图),
将正方体切去两个正三棱锥![]() 和
和![]() ,得到一个几何体
,得到一个几何体![]() ,
,![]() 是以平行平面
是以平行平面![]() 和
和![]() 为上下底,每个侧面都是直角等腰三角形,截面多边形
为上下底,每个侧面都是直角等腰三角形,截面多边形![]() 的每一条边分别与
的每一条边分别与![]() 的底面上的一条边平行,设正方体棱长为
的底面上的一条边平行,设正方体棱长为![]() ,
,![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,同理可证明
,同理可证明![]() ,故六边形
,故六边形![]() 的周长为
的周长为![]() ,即周长为定值;
,即周长为定值;
当![]() 都在对应棱的中点时,
都在对应棱的中点时,![]() 是正六边形,计算可得面积
是正六边形,计算可得面积![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,当
,当![]() 无限趋近于
无限趋近于![]() 时,
时,![]() 的面积无限趋近于
的面积无限趋近于![]() ,故
,故![]() 的面积一定会发生变化,不为定值。
的面积一定会发生变化,不为定值。
故答案为B.

【题目】为探索课堂教学改革,惠来县某中学数学老师用传统教学和“导学案”两种教学方式,在甲、乙两个平行班进行教学实验.为了解教学效果,期末考试后,分别从两个班级各随机抽取20名学生的成绩进行统计,得到如下茎叶图.记成绩不低于70分者为“成绩优良”.
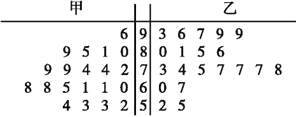
(Ⅰ)分析甲、乙两班的样本成绩,大致判断哪种教学方式的教学效果更佳,并说明理由;
(Ⅱ)由以上统计数据完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩是否优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
参考公式:![]() ,其中
,其中![]() 是样本容量.
是样本容量.
独立性检验临界值表:

【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
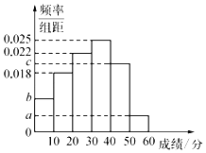
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: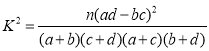 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |