题目内容
已知定义在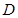 上的函数
上的函数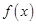 ,如果满足:对任意
,如果满足:对任意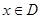 ,存在常数
,存在常数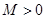 ,使得
,使得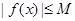 成立,则称
成立,则称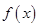 是
是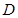 上的有界函数,其中
上的有界函数,其中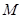 称为函数
称为函数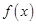 的上界.
的上界.
下面我们来考虑两个函数: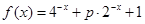 ,
,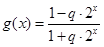 .
.
(Ⅰ)当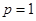 时,求函数
时,求函数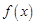 在
在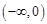 上的值域,并判断函数
上的值域,并判断函数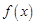 在
在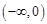 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若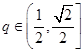 ,函数
,函数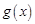 在
在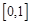 上的上界是
上的上界是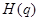 ,求
,求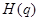 的取值范围;
的取值范围;
(Ⅲ)若函数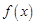 在
在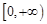 上是以
上是以 为上界的有界函数, 求实数
为上界的有界函数, 求实数 的取值范围.
的取值范围.
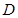 上的函数
上的函数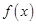 ,如果满足:对任意
,如果满足:对任意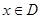 ,存在常数
,存在常数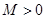 ,使得
,使得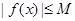 成立,则称
成立,则称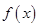 是
是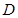 上的有界函数,其中
上的有界函数,其中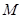 称为函数
称为函数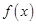 的上界.
的上界.下面我们来考虑两个函数:
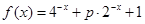 ,
,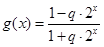 .
.(Ⅰ)当
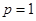 时,求函数
时,求函数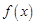 在
在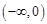 上的值域,并判断函数
上的值域,并判断函数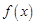 在
在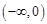 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(Ⅱ)若
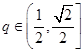 ,函数
,函数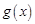 在
在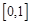 上的上界是
上的上界是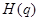 ,求
,求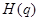 的取值范围;
的取值范围;(Ⅲ)若函数
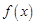 在
在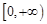 上是以
上是以 为上界的有界函数, 求实数
为上界的有界函数, 求实数 的取值范围.
的取值范围.(Ⅰ)函数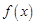 在
在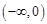 上的值域为
上的值域为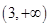 ,函数
,函数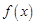 在
在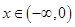 不是有界函数;(Ⅱ)
不是有界函数;(Ⅱ)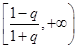 ;(Ⅲ)
;(Ⅲ)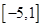 .
.
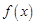 在
在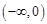 上的值域为
上的值域为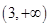 ,函数
,函数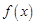 在
在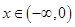 不是有界函数;(Ⅱ)
不是有界函数;(Ⅱ)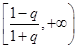 ;(Ⅲ)
;(Ⅲ)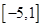 .
.试题分析:(Ⅰ)当
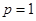 时,函数
时,函数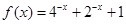 ,此时可设
,此时可设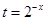 ,由
,由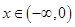 ,那么
,那么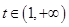 ,所以函数
,所以函数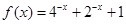 可转化成
可转化成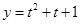 ,易知
,易知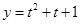 在
在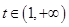 上单调递增,从而可求出值域为
上单调递增,从而可求出值域为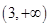 ;故不存在常数
;故不存在常数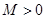 ,使
,使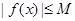 成立,所以函数
成立,所以函数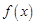 在
在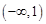 上不是有界函数
上不是有界函数(Ⅱ)先求出
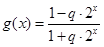 在
在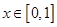 上的最大值
上的最大值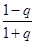 与最小值
与最小值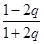 ,根据
,根据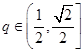 ,再确定
,再确定
 的大小关系,得出上界范围
的大小关系,得出上界范围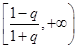 ;(Ⅲ)函数
;(Ⅲ)函数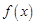 在
在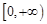 上是以
上是以 为上界的有界函数,则
为上界的有界函数,则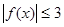 在
在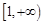 上恒成立.将问题转化成
上恒成立.将问题转化成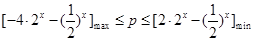 而求得
而求得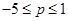 .
.试题解析:(Ⅰ)当
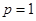 时,
时,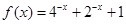
因为
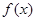 在
在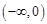 上递减,所以
上递减,所以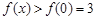 ,即
,即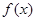 在
在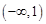 的值域为
的值域为 .
.故不存在常数
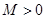 ,使
,使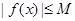 成立,所以函数
成立,所以函数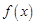 在
在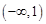 上不是有界函数.
上不是有界函数.(Ⅱ)
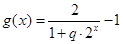 ,∵
,∵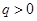 ,
,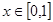 ∴
∴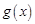 在
在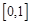 上递减,
上递减,∴
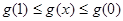 即
即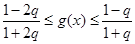
∵
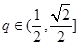 ,∴
,∴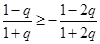 ,∴
,∴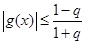 ,
,∴
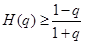 ,即
,即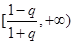
(Ⅲ)由题意知,
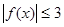 在
在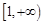 上恒成立.
上恒成立.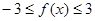 ,∴
,∴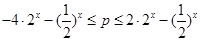 在
在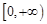 上恒成立
上恒成立∴
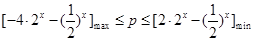
设
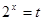 ,
,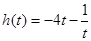 ,
,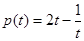 , 由
, 由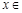
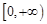 得
得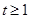 ,
,设
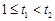 ,
, , 所以
, 所以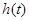 在
在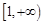 上递减,
上递减,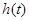 在
在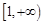 上的最大值为
上的最大值为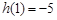 ,
,又
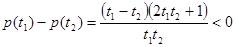 ,所以
,所以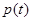 在
在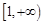 上递增,
上递增,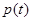 在
在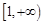 上的最小值为
上的最小值为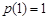 .
.所以实数
 的取值范围为
的取值范围为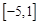 .
.
练习册系列答案
相关题目
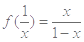 ,则当
,则当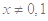 时,
时, ( )
( )
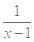
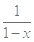
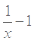
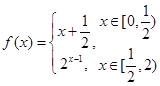 ,若存在
,若存在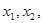 当
当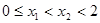 时,
时,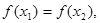 则
则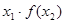 的取值范围是
的取值范围是  的定义域为
的定义域为 ,部分对应值如表.
,部分对应值如表.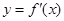 的图象如图所示.下列关于函数
的图象如图所示.下列关于函数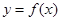 是周期函数;②函数
是周期函数;②函数 是减函数;③如果当
是减函数;③如果当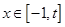 时,
时, 的最大值为4;④当
的最大值为4;④当 时,函数
时,函数 有4个零点.其中真命题的个数是 .
有4个零点.其中真命题的个数是 .
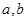 ,定义运算“
,定义运算“ ”:
”: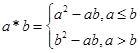 ,设
,设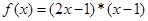 ,且关于x的方程
,且关于x的方程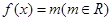 恰有三个互不相等的实数根
恰有三个互不相等的实数根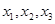 ,则
,则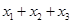 的取值范围是____________.
的取值范围是____________.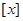 表示不大于
表示不大于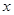 的最大整数,则函数
的最大整数,则函数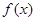 =lg2x-[lgx]-2的零点个数( )个
=lg2x-[lgx]-2的零点个数( )个 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
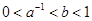



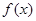 满足
满足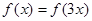 ,当
,当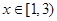 ,
,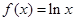 ,若在区间
,若在区间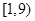 内,函数
内,函数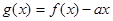 有三个不同零点,则实数
有三个不同零点,则实数 的取值范围是( )
的取值范围是( )
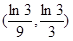
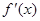 和
和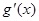 分别是
分别是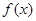 和
和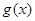 的导函数,若
的导函数,若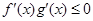 在区间
在区间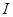 上恒成立,则称
上恒成立,则称 与
与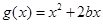 在开区间
在开区间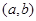 上单调性相反(
上单调性相反(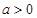 ),则
),则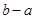 的最大值为 .
的最大值为 .