题目内容
已知函数
的图象如图所示，则
满足的关系是（ ）
的图象如图所示，则满足的关系是（ ）A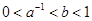． | B． |
C． | D． |
A
试题分析：
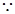函数
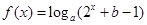是随着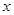
的增大而增大，
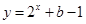也是随着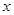的增大而增大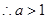
，
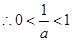
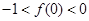
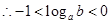
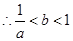
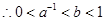故选
.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
试题分析：
函数是随着的增大而增大，也是随着的增大而增大，故选.千里马走向假期期末仿真试卷寒假系列答案题目内容
的图象如图所示，则满足的关系是（ ）| A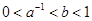． | B． |
| C． | D． |
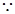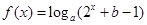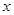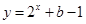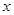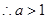
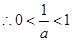
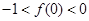
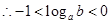
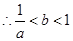
函数是随着的增大而增大，也是随着的增大而增大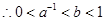，故选.千里马走向假期期末仿真试卷寒假系列答案
，按每年
衰减.
年后，这种放射性元素的质量
与
的函数关系式；
时所经历的时间）.（
）
上的函数
，如果满足：对任意
，存在常数
，使得
成立，则称
是
称为函数
，
.
时，求函数
在
上的值域，并判断函数
，函数
在
上的上界是
，求
上是以
为上界的有界函数， 求实数
的取值范围．
与服药后的时间
之间近似满足如图所示的曲线．其中
是线段，曲线段
是函数
是常数
的图象．
关于时间
的函数关系式；
时治疗有效，假若某病人第一次服药为早上
，为保持疗效，第二次服药最迟是当天几点钟？
，该病人每毫升血液中含药量为多少
？
（其中
为常数且 
）的图象经过点
.
的解析式；
在
上恒成立，求实数
的取值范围.
m,盖子边长为
m,
千件并全部销售完，每千件的销售收入为
万元，且
．
（万元）关于年产量
，
，函数
满足
”
的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
关于原点的中心对称点的组数为_____________