题目内容
(本小题满分13分)
(1)证明：函数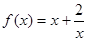
在
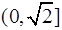上是减函数，在[
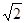，+∞)上是增函数；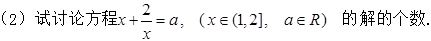
解： （1）证明：见解析；
（2）当
时，方程无解；当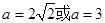
方程有一个解；当
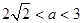时，方程有两个解.
解析
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
口算题卡北京妇女儿童出版社系列答案题目内容
(本小题满分13分)
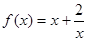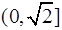(1)证明：函数在上是减函数，在[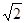，+∞)上是增函数；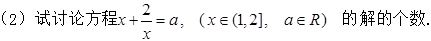
解： （1）证明：见解析；
（2）当时，方程无解；当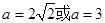方程有一个解；当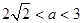时，方程有两个解.
解析
口算题卡北京妇女儿童出版社系列答案
.
为何实数
总是为增函数；
，（
且
）。
，令
，试判断函数
在
上的单调性并证明你的结论；
且
的定义域和值域都是
的最大值；
对
恒成立，求实数
的取值范围； 
是奇函数. 
的值；
在区间
上单调递增，求实数
的取值范围. 
是定义在（–1，1）上的奇函数，且
. 
的函数
都有
；
时，
，回答下列问题：
的单调性，并说明理由；
，求
的值. 
，
的一个极值点，求a的值；
上是增函数；
总存在
成立，求实数m的取值范围。
的定义域和値域.