题目内容
对于在区间 [ m,n ] 上有意义的两个函数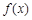 与
与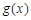 ,如果对任意
,如果对任意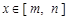 ,均有
,均有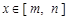 ,则称
,则称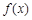 与
与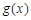 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称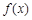 与
与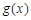 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数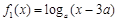 与
与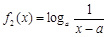 (a > 0且
(a > 0且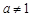 ),给定区间
),给定区间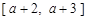 .
.
(1)若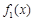 与
与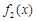 在给定区间
在给定区间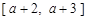 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论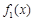 与
与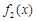 在给定区间
在给定区间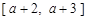 上是否友好.
上是否友好.
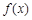 与
与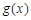 ,如果对任意
,如果对任意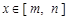 ,均有
,均有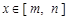 ,则称
,则称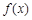 与
与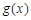 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称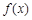 与
与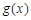 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数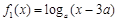 与
与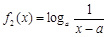 (a > 0且
(a > 0且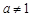 ),给定区间
),给定区间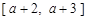 .
.(1)若
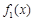 与
与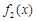 在给定区间
在给定区间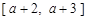 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;(2)讨论
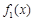 与
与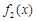 在给定区间
在给定区间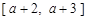 上是否友好.
上是否友好.(1) 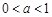 ;(2) 当
;(2) 当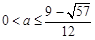 时,
时, 在
在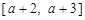 上是友好的,当
上是友好的,当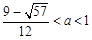 时,
时, 在
在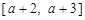 上是不友好的
上是不友好的
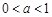 ;(2) 当
;(2) 当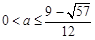 时,
时, 在
在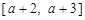 上是友好的,当
上是友好的,当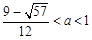 时,
时, 在
在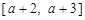 上是不友好的
上是不友好的试题分析:(1)函数f(x)与g(x)在区间[a+2,a+3]上有意义,必须满足
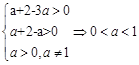 (2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,
(2)假设存在实数a,使得函数f(x)与g(x)在区间[a+2,a+3]上是“友好”的,则|f(x)-g(x)|=|loga(x2-4ax+3a2)|⇒|loga(x2-4ax+3a2)|≤1即-1≤loga(x2-4ax+3a2)≤1(*),因为a∈(0,1)⇒2a∈(0,2),而[a+2,a+3]在x=2a的右侧,
所以函数g(x)=loga(x2-4ax+3a2)在区间[a+2,a+3]上为减函数,从而
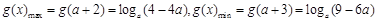 ,于是不等式(*)成立的充要条件是
,于是不等式(*)成立的充要条件是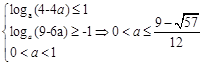 ,因此,当
,因此,当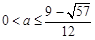 时,
时, 在
在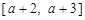 上是友好的; 当
上是友好的; 当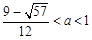 时,
时, 在
在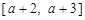 上是不友好的
上是不友好的点评:此类问题要求学生熟练掌握函数单调性的判断与证明,以及新定义的运用,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
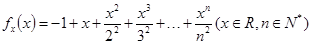 ,证明:
,证明: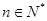 ,存在唯一的
,存在唯一的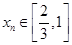 ,满足
,满足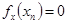 ;
;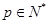 ,由(Ⅰ)中
,由(Ⅰ)中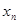 构成的数列
构成的数列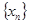 满足
满足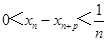 .
.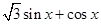
 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 (千克/年);当
(千克/年);当 时,
时, (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, (千克/年).
(千克/年). 时,求函数
时,求函数 的表达式;
的表达式; 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.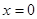 是函数
是函数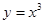 的极值点;
的极值点;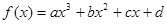 有极值点的充要条件是
有极值点的充要条件是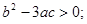
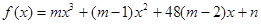 在区间
在区间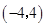 上单调递减.
上单调递减.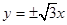 ,则其离心率为2.
,则其离心率为2.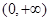 上是增函数的是( )
上是增函数的是( )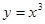
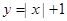
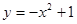
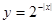
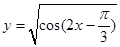 的定义域是 .
的定义域是 . 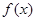 是定义在
是定义在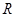 上的奇函数,在
上的奇函数,在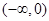 上为减函数,且
上为减函数,且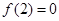 ,则使得
,则使得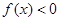 的
的 的取值范围是 ( )
的取值范围是 ( ) 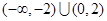
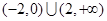

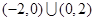
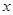 %,则销售量将减少
%,则销售量将减少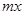 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过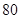 %,
%,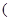 其中
其中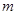 为正常数
为正常数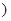

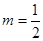 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?