题目内容
若函数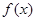 是定义在
是定义在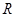 上的奇函数,在
上的奇函数,在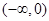 上为减函数,且
上为减函数,且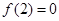 ,则使得
,则使得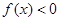 的
的 的取值范围是 ( )
的取值范围是 ( )
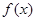 是定义在
是定义在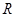 上的奇函数,在
上的奇函数,在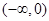 上为减函数,且
上为减函数,且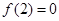 ,则使得
,则使得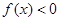 的
的 的取值范围是 ( )
的取值范围是 ( ) A.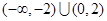 | B.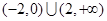 |
C. | D.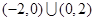 |
B
试题分析:解:∵函数f(x)是定义在R上的奇函数,在(-∞,0)上是减函数,∴函数f(x)是在(0,,+∞)上是减函数,∴x>0,则
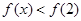 或∴x<0,则
或∴x<0,则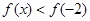 ,∴x的取值范围是(-2,0)∪(2,+∞),故答案为B
,∴x的取值范围是(-2,0)∪(2,+∞),故答案为B点评:本题主要考查不等式的解法,考查函数单调性与奇偶性的结合,应注意奇函数在其对称区间上单调性相同,偶函数在其对称区间上单调性相反.

练习册系列答案
相关题目
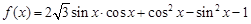 (
(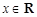 )
)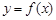 的周期和递增区间;
的周期和递增区间;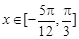 ,求
,求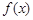 的取值范围.
的取值范围.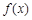 与
与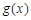 ,如果对任意
,如果对任意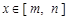 ,均有
,均有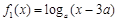 与
与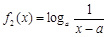 (a > 0且
(a > 0且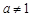 ),给定区间
),给定区间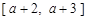 .
.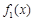 与
与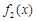 在给定区间
在给定区间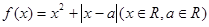 .
.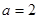 时,求
时,求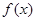 的单调区间;
的单调区间;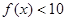 对
对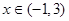 恒成立,求实数
恒成立,求实数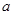 的取值范围.
的取值范围.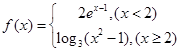 则不等式
则不等式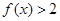 的解集为( )
的解集为( )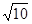 ,+∞)
,+∞)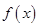 满足
满足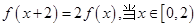 时,
时,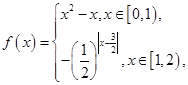 若
若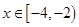 时,
时,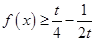 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是



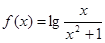 ,有下列结论:①函数
,有下列结论:①函数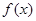 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数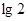 ;④当
;④当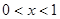 时,函数
时,函数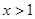 时,函数
时,函数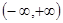 上的偶函数
上的偶函数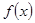 满足
满足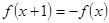 ,且在
,且在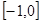 上是增函数,下面关于
上是增函数,下面关于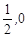 )对称 ②
)对称 ②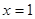 对称;
对称;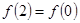 .
.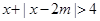 恒成立,则实数
恒成立,则实数 的取值范围是:_ .
的取值范围是:_ .