题目内容
设函数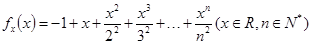 ,证明:
,证明:
(Ⅰ)对每个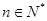 ,存在唯一的
,存在唯一的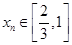 ,满足
,满足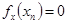 ;
;
(Ⅱ)对任意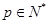 ,由(Ⅰ)中
,由(Ⅰ)中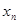 构成的数列
构成的数列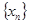 满足
满足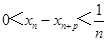 .
.
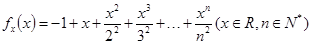 ,证明:
,证明:(Ⅰ)对每个
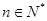 ,存在唯一的
,存在唯一的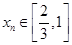 ,满足
,满足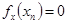 ;
;(Ⅱ)对任意
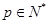 ,由(Ⅰ)中
,由(Ⅰ)中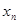 构成的数列
构成的数列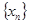 满足
满足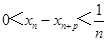 .
.见解析
(1)对每个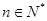 ,当
,当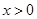 时,
时,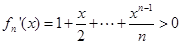 ,
,
则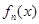 在
在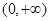 内单调递增,
内单调递增,
而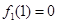 ,当
,当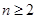 时,
时,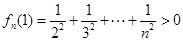 ,
,
故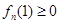 ,
,
又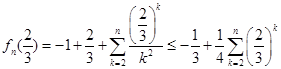
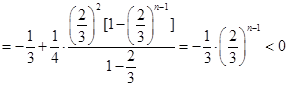
所以对每个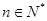 ,存在唯一的
,存在唯一的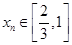 ,满足
,满足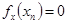
当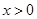 时,
时,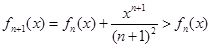 ,并由(1)知
,并由(1)知
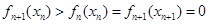
由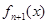 在
在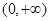 内单调递增知,
内单调递增知,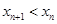 ,故
,故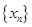 为单调递减数列,
为单调递减数列,
从而对任意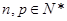 ,
,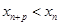
对任意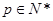 ,
,
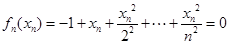 ①
①
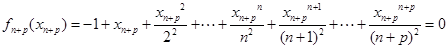 ②
②
①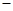 ②并移项,利用
②并移项,利用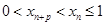 ,得
,得
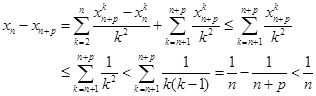
因此,对任意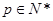 ,
,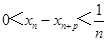 .
.
本题考查的是数列函数,而且含双变量,考生在做题的过程中需要冷静的处理好每个变量.第(1)题考查函数的零点问题,要证明对每个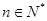 ,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断
,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断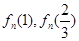 的正负问题,此题难点在于判断
的正负问题,此题难点在于判断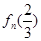 的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由
的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由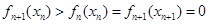 ,
,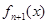 在
在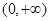 内单调递增,确定
内单调递增,确定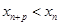 ,则不等式左半边成立,右半边通过作差,数列放缩确定最终
,则不等式左半边成立,右半边通过作差,数列放缩确定最终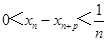 .本题属于较难题.
.本题属于较难题.
【考点定位】考查函数的导数及其应用,函数零点的判定,等比数列的求和,不等式的放缩等知识.
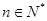 ,当
,当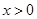 时,
时,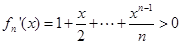 ,
,则
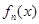 在
在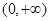 内单调递增,
内单调递增,而
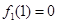 ,当
,当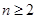 时,
时,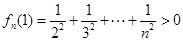 ,
,故
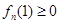 ,
,又
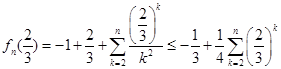
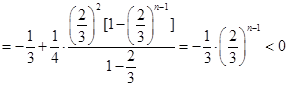
所以对每个
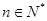 ,存在唯一的
,存在唯一的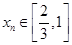 ,满足
,满足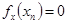
当
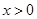 时,
时,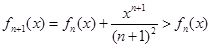 ,并由(1)知
,并由(1)知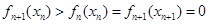
由
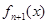 在
在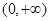 内单调递增知,
内单调递增知,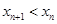 ,故
,故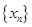 为单调递减数列,
为单调递减数列,从而对任意
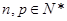 ,
,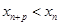
对任意
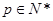 ,
,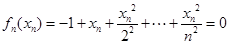 ①
①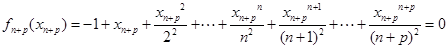 ②
②①
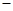 ②并移项,利用
②并移项,利用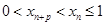 ,得
,得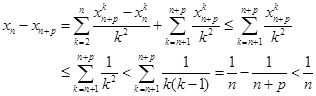
因此,对任意
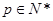 ,
,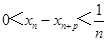 .
.本题考查的是数列函数,而且含双变量,考生在做题的过程中需要冷静的处理好每个变量.第(1)题考查函数的零点问题,要证明对每个
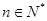 ,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断
,函数在某个区间上只有一个零点,一方面要证明函数是单调的,求导即可,另一方面要判断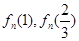 的正负问题,此题难点在于判断
的正负问题,此题难点在于判断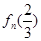 的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由
的正负时,要利用放缩的思想,将这个数列函数放缩到可以利用等比数列求和,从而证明此函数在指定区间内只有一个零点;第(2)题要将数列从数列函数中分离出来,就要通过函数的单调性,由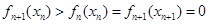 ,
,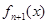 在
在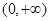 内单调递增,确定
内单调递增,确定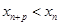 ,则不等式左半边成立,右半边通过作差,数列放缩确定最终
,则不等式左半边成立,右半边通过作差,数列放缩确定最终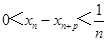 .本题属于较难题.
.本题属于较难题.【考点定位】考查函数的导数及其应用,函数零点的判定,等比数列的求和,不等式的放缩等知识.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
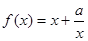 定义域为
定义域为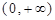 ,且
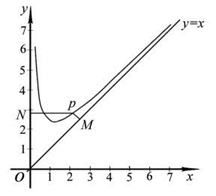
,且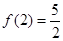 .设点
.设点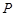 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点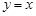 和
和 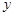 轴的垂线,垂足分别为
轴的垂线,垂足分别为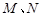 .
.
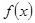 的单调递减区间(不必证明);
的单调递减区间(不必证明);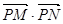 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由; 为坐标原点,求四边形
为坐标原点,求四边形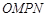 面积的最小值.
面积的最小值.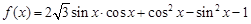 (
(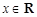 )
)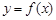 的周期和递增区间;
的周期和递增区间;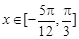 ,求
,求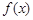 的取值范围.
的取值范围.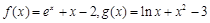 . 若实数a, b满足
. 若实数a, b满足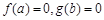 , 则( )
, 则( )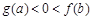
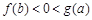

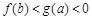
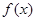 是定义在
是定义在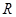 上的奇函数. 当
上的奇函数. 当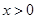 时,
时,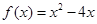 ,则不等式
,则不等式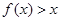 的解集用区间表示为
的解集用区间表示为 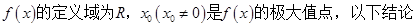 一定正确的是( )
一定正确的是( )



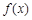 与
与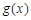 ,如果对任意
,如果对任意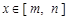 ,均有
,均有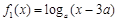 与
与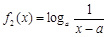 (a > 0且
(a > 0且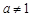 ),给定区间
),给定区间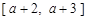 .
.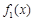 与
与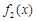 在给定区间
在给定区间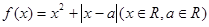 .
.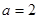 时,求
时,求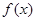 的单调区间;
的单调区间;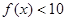 对
对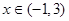 恒成立,求实数
恒成立,求实数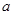 的取值范围.
的取值范围.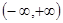 上的偶函数
上的偶函数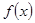 满足
满足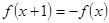 ,且在
,且在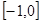 上是增函数,下面关于
上是增函数,下面关于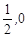 )对称 ②
)对称 ②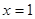 对称;
对称;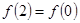 .
.