题目内容
1.已知定义在R上的偶函数f(x)满足对任意x∈R都有f(x+4)=f(x),且当x∈[-2,0]时,$f(x)={(\frac{1}{2})^x}-1$.若在区间x∈(-2,6)内函数g(x)=f(x)-loga(x+2)有3个不同的零点,则实数a的取值范围为($\root{3}{4}$,2).分析 由题意可得,分别画出y=f(x)和y=loga(x+2)的图象,数形结合求得a的范围.
解答 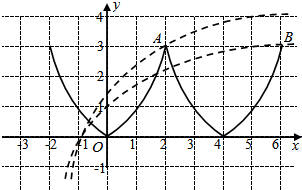 解:∵偶函数f(x)满足对任意x∈R都有f(x+4)=f(x),
解:∵偶函数f(x)满足对任意x∈R都有f(x+4)=f(x),
∴函数f(x)的周期为4,
当x∈[-2,0]时,$f(x)={(\frac{1}{2})^x}-1$,
∴x∈[0,2]时,f(x)=2x-1,
分别画出y=f(x)和y=loga(x+2)的图象,
在区间x∈(-2,6)内,
如图所示,函数y=loga(x+2)的图象过定点(-1,0),
当y=loga(x+2)的图象可点A时,即3=loga(2+2),即a=$\root{3}{4}$时,有2个零点,
当y=loga(x+2)的图象可点B时,即3=loga(2+6),即a=2,有3个零点,
∵在区间x∈(-2,6)内函数g(x)=f(x)-loga(x+2)有3个不同的零点,
∴$\root{3}{4}$<a≤2,
故a的取值范围为($\root{3}{4}$,2],
故答案为:($\root{3}{4}$,2].
点评 本题主要考查函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
11.已知抛物线的方程为y2=4x,过其焦点F的宜线l与抛物线交于A,B两点,若S△AOF=S△BOF(O为坐标原点),则|AB|=( )
| A. | $\frac{16}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | 4 |
13.某校从6名教师中选派3名教师同时去3个贫困地区支教,每个地区1人,其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案有( )
| A. | 24种 | B. | 42种 | C. | 36种 | D. | 48种 |