题目内容
13.某校从6名教师中选派3名教师同时去3个贫困地区支教,每个地区1人,其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案有( )| A. | 24种 | B. | 42种 | C. | 36种 | D. | 48种 |
分析 先从6名教师中选出3名,因为甲和乙不同去,甲和丙只能同去或同不去,所以可按选甲和不选甲分成两类,两类方法数相加,再把3名老师分配去3个边远地区支教,3名教师进行全排列即可.
解答 解:根据题意,分两步进行分析:
①、先从6名教师中选出三名老师,
又分需分2类进行讨论
1、甲去,则丙一定去,乙一定不去,有C31=3种不同选法
2、甲不去,则丙一定不去,乙可能去也可能不去,有C43=4种不同选法,
∴不同的选法有3+4=7种
②、将选出的三名老师全排列,对应3个地区,有A33=6种情况,
根据分步计数原理得不同的选派方案共有,7×6=42.
故选:B.
点评 本题考查了排列组合的综合应用,关键是审清题意,明确条件、事件之间的关系,要分清用排列还是用组合去做.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.将y=sin(2x-$\frac{π}{6}$)图象向右平移$\frac{π}{12}$个单位,所得函数图象的一条对称轴的方程是( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=-$\frac{π}{12}$ |
3.如图是“推理与证明”的知识结构图,如果要加入“归纳”,则应该放在( )

| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
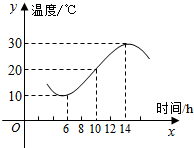 如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).
如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).