题目内容
10.已知函数f(x)=2sin(2x-$\frac{π}{4}$).(1)求函数的最值及相应的x值集合;
(2)求函数的单调区间;
(3)求函数f(x)的图象的对称轴与对称中心.
分析 (1)根据正弦函数的最值性质即可求函数的最值及相应的x值集合;
(2)根据三角函数的单调性即可求函数的单调区间;
(3)根据三角函数的对称性即可求函数f(x)的图象的对称轴与对称中心.
解答 解:(1)当sin(2x-$\frac{π}{4}$)=1,即2x-$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z,
即x=kπ+$\frac{3π}{8}$,k∈Z,此时函数取得最大值为2;
故f(x)的最大值为2,使函数取得最大值的x的集合为{x|x=$\frac{3π}{8}$+kπ,k∈Z};
(2)由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,得-$\frac{π}{8}$+kπ≤x≤$\frac{3π}{8}$+kπ,k∈Z.
∴函数f(x)的单调递增区间为[-$\frac{π}{8}$+kπ,$\frac{3π}{8}$+kπ],k∈Z.
由$\frac{π}{2}$+2kπ≤2x-$\frac{π}{4}$≤$\frac{3π}{2}$+2kπ,得$\frac{3π}{8}$+kπ≤x≤$\frac{5π}{8}$+kπ,k∈Z.
∴函数f(x)的单调递减区间为[$\frac{3π}{8}$+kπ,$\frac{5π}{8}$+kπ],k∈Z.
(3)由2x-$\frac{π}{4}$=$\frac{π}{2}$+kπ,得x=$\frac{3π}{8}$+$\frac{1}{2}$kπ,k∈Z.
即函数f(x)的图象的对称轴为x=$\frac{3π}{8}$+$\frac{1}{2}$kπ,k∈Z.
由2x-$\frac{π}{4}$=kπ,得x=$\frac{π}{8}$+$\frac{1}{2}$kπ,k∈Z.即对称中心为($\frac{π}{8}$+$\frac{1}{2}$kπ,0),k∈Z..
点评 本题考查了y=Asin(ωx+φ)型函数的性质,关键是学生应熟悉教材基本内容,是中档题.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
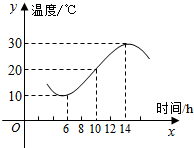 如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).
如图,某地一天从6时到14时的温度变化曲线近似满足函数f(x)=Asin(ωx+φ)+b,(A>0,ω>0,0<φ<π).