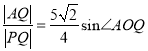题目内容
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,以
,以![]() 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以![]() 为圆心以1为半径的圆相交,且交点在椭圆
为圆心以1为半径的圆相交,且交点在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
(i)求![]() 的值;
的值;
(ⅱ)求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)2;(ⅱ)
;(Ⅱ)(i)2;(ⅱ)![]() .
.
【解析】
试题(Ⅰ)根据椭圆的定义与几何性质列方程组确定![]() 的值,从而得到椭圆
的值,从而得到椭圆![]() 的方程;(Ⅱ)(i)设
的方程;(Ⅱ)(i)设![]() ,
,![]() ,由题意知
,由题意知![]() ,然后利用这两点分别在两上椭圆上确定
,然后利用这两点分别在两上椭圆上确定![]() 的值; (ⅱ)设
的值; (ⅱ)设![]() ,利用方程组
,利用方程组 结合韦达定理求出弦长
结合韦达定理求出弦长![]() ,选将
,选将![]() 的面积表示成关于
的面积表示成关于![]() 的表达式
的表达式![]()
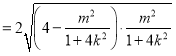 ,然后,令
,然后,令![]() ,利用一元二次方程根的判别式确定的范围,从而求出
,利用一元二次方程根的判别式确定的范围,从而求出![]() 的面积的最大值,并结合(i)的结果求出
的面积的最大值,并结合(i)的结果求出![]() 面积的最大值.
面积的最大值.
试题解析:(Ⅰ)由题意知![]() ,则
,则![]() ,又
,又![]() 可得
可得![]() ,
,
所以椭圆C的标准方程为![]() .
.
(Ⅱ)由(Ⅰ)知椭圆E的方程为![]() ,
,
(i)设![]() ,
,![]() ,由题意知
,由题意知![]() 因为
因为![]() ,
,
又![]() ,即
,即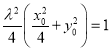 ,所以
,所以![]() ,即
,即![]() .
.
(ⅱ)设![]()
将![]() 代入椭圆E的方程,
代入椭圆E的方程,
可得![]()
由![]() ,可得
,可得![]() ①
①
则有![]()
所以![]()
因为直线![]() 与轴交点的坐标为
与轴交点的坐标为![]()
所以![]() 的面积
的面积![]()
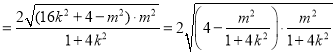
令![]() ,将
,将![]() 代入椭圆C的方程可得
代入椭圆C的方程可得![]()
由![]() ,可得
,可得![]() ②
②
由①②可知![]()
因此![]() ,故
,故![]()
当且仅当![]() ,即
,即![]() 时取得最大值
时取得最大值![]()
由(i)知,![]() 面积为
面积为![]() ,所以
,所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目