题目内容
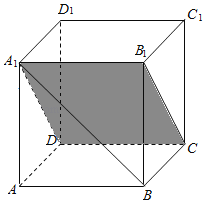
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. 
(1)求证:AA1⊥平面ABC;
(2)求证二面角A1﹣BC1﹣B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求 ![]() 的值.
的值.
【答案】
(1)证明:∵AA1C1C是正方形,∴AA1⊥AC.
又∵平面ABC⊥平面AA1C1C,平面ABC∩平面AA1C1C=AC,
∴AA1⊥平面ABC.
(2)解:由AC=4,BC=5,AB=3.
∴AC2+AB2=BC2,∴AB⊥AC.
建立如图所示的空间直角坐标系,则A1(0,0,4),B(0,3,0),B1(0,3,4),C1(4,0,4),
∴ ![]() ,
, ![]() ,
, ![]() .
.
设平面A1BC1的法向量为 ![]() ,平面B1BC1的法向量为
,平面B1BC1的法向量为 ![]() =(x2,y2,z2).
=(x2,y2,z2).
则  ,令y1=4,解得x1=0,z1=3,∴
,令y1=4,解得x1=0,z1=3,∴ ![]() .
.
 ,令x2=3,解得y2=4,z2=0,∴
,令x2=3,解得y2=4,z2=0,∴ ![]() .
.
![]() =
=  =
= ![]() =
= ![]() .
.
∴二面角A1﹣BC1﹣B1的余弦值为 ![]() .
.
(3)证明:设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D ![]() ,
,
∴ ![]() =
= ![]() ,
, ![]() =(0,3,﹣4),
=(0,3,﹣4),
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,解得t=
,解得t= ![]() .
.
∴ ![]() .
.

【解析】(1)利用AA1C1C是正方形,可得AA1⊥AC,再利用面面垂直的性质即可证明;(2)利用勾股定理的逆定理可得AB⊥AC.通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得到二面角;(3)设点D的竖坐标为t,(0<t<4),在平面BCC1B1中作DE⊥BC于E,可得D ![]() ,利用向量垂直于数量积得关系即可得出.
,利用向量垂直于数量积得关系即可得出.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

【题目】随着支付宝、微信等支付方式的上线,越来越多的商业场景可以实现手机支付.有关部门为了了解各年龄段的人使用手机支付的情况,随机调查了50次商业行为,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
手机支付 | 4 | 6 | 10 | 6 | 2 | 0 |
(1)若把年龄在![]() 的人称为中青年,年龄在
的人称为中青年,年龄在![]() 的人称为中老年,请根据上表完成以下
的人称为中老年,请根据上表完成以下![]() 列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
手机支付 | 未使用手机支付 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
(2)若从年龄在![]() 的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为
的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.15 | 0.10 | 0.005 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |