题目内容
【题目】随着支付宝、微信等支付方式的上线,越来越多的商业场景可以实现手机支付.有关部门为了了解各年龄段的人使用手机支付的情况,随机调查了50次商业行为,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
手机支付 | 4 | 6 | 10 | 6 | 2 | 0 |
(1)若把年龄在![]() 的人称为中青年,年龄在
的人称为中青年,年龄在![]() 的人称为中老年,请根据上表完成以下
的人称为中老年,请根据上表完成以下![]() 列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
手机支付 | 未使用手机支付 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
(2)若从年龄在![]() 的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为
的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.15 | 0.10 | 0.005 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)不能(2)见解析
【解析】分析:(1)根据题意完成![]() 列联表,求出
列联表,求出![]() ,然后进行判断;
,然后进行判断;
(2)利用超几何分布可求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
详解:
(1)2×2列联表如图所示:
手机支付 | 未使用手机支付 | 总计 | |
中青年 | 20 | 10 | 30 |
中老年 | 8 | 12 | 20 |
总计 | 28 | 22 | 50 |
![]()
所以在犯错误的概率不超过![]() 的前提下不能认为使用手机支付与年龄(中青年、中老年)有关系.
的前提下不能认为使用手机支付与年龄(中青年、中老年)有关系.
(2)年龄在![]() 的被调查者共
的被调查者共![]() 人,其中使用手机支付的有
人,其中使用手机支付的有![]() 人,则抽取的
人,则抽取的![]() 人中使用手机支付的人数
人中使用手机支付的人数![]() 可能取值为
可能取值为![]() ,
,
则 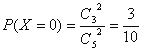 ;
;
 ;
;

所以X的分布列为:
X | 0 | 1 | 2 |
|
|
|
|
![]() .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
是否需要志愿者 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


