题目内容
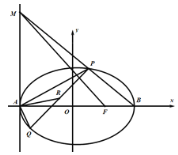
【题目】已知抛物线y2=2px（p＞0），其准线方程为x+1=0，直线l过点T（t，0）（t＞0）且与抛物线交于A、B两点，O为坐标原点．
（1）求抛物线方程，并证明： 
的值与直线l倾斜角的大小无关；
（2）若P为抛物线上的动点，记|PT|的最小值为函数d（t），求d（t）的解析式．
【答案】
（1）解：由题意可知：准线方程x=﹣1，则﹣ 
=﹣1，则p=2，
∴抛物线的标准方程为：y2=4x，
证明：若直线l的斜率不存在，则其方程为x=t，代入y2=4x得，A（t，2 
），B（t，﹣2 ），
则 
=t2﹣4t，
则若直线l的斜率存在，设其斜率为 
（k≠0），则l的方程为x=my+t，
联立 
，整理得：y2﹣4ky﹣4t=0．
设A（x1，y1），B（x2，y2），则y1+y2=4k，y1y2=﹣4t，
x1x2=（my1+t）（my2+t）=m2y1y2+mt（y1+y2）+t2=t2．
=x1x2+y1y2=t2﹣4t，
综上， 的值t2﹣4t与直线l倾斜角的大小无关
（2）解：设P（x，2 
），则丨PT丨2=（x﹣t）2+（2 ﹣0）2=x2﹣2（t﹣2）x+t2，（x＞0），
由二次函数的性质可知：当对称轴x=t﹣2＜0，即0＜t＜2时，当x=0时，丨PT丨取最小值，最小值为t，
当t﹣2≥0时，即x=t﹣2时，取最小值，丨PT丨取最小值，最小值为2 
，
d（t）的解析式，d（t）= 
【解析】（1）由题意可知p=2，求得抛物线方程，当直线斜率存在时，代入抛物线方程，利用韦达定理及向量数量积的坐标运算，即可求得 的值与直线l倾斜角的大小无关；（2）利用点到直线的距离公式及二次函数的性质即可求得|PT|的最小值，求得d（t）的解析式．
练习册系列答案
相关题目
