题目内容
【题目】已知函数f（x）=sinωx﹣ 
cosωx（ω＞0），若方程f（x）=﹣1在（0，π）上有且只有四个实数根，则实数ω的取值范围为（ ）
A.（ 
， 
]
B.（ ， 
]
C.（ ， 
]
D.（ ， 
]
【答案】B
【解析】解：f（x）=2sin（ωx﹣ 
）， 作出f（x）的函数图象如图所示：
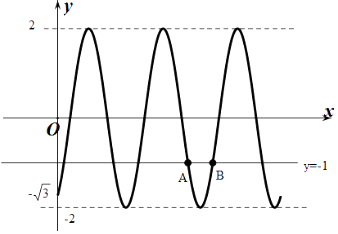
令2sin（ωx﹣ ）=﹣1得ωx﹣ =﹣ 
+2kπ，或ωx﹣ = 
+2kπ，
∴x= 
+ 
，或x= 
+ ，kZ，
设直线y=﹣1与y=f（x）在（0，+∞）上从左到右的第4个交点为A，第5个交点为B，
则xA= 
，xB= 
，
∵方程f（x）=﹣1在（0，π）上有且只有四个实数根，
∴xA＜π≤xB ，
即 ＜π≤ ，解得 
．
故选B．
化简f（x）的解析式，作出f（x）的函数图象，利用三角函数的性质求出直线y=﹣1与y=f（x）在（0，+∞）上的交点坐标，则π介于第4和第5个交点横坐标之间．
练习册系列答案
相关题目
