题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处有极值
处有极值![]() ,求
,求![]() 的值;
的值;
(2)若对于任意的![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:(1)由![]() ,根据题意设有
,根据题意设有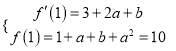 解得
解得![]() 或
或![]() ,进行检验舍去
,进行检验舍去![]() 得所求b值;(2)由题意知
得所求b值;(2)由题意知![]() 对任意的
对任意的![]() 都成立,所以
都成立,所以![]() 对任意的
对任意的![]() 都成立,因为
都成立,因为![]() ,所以
,所以![]() 在
在![]() 上为单调增函数或为常数函数,①当
上为单调增函数或为常数函数,①当![]() 为常数函数时,
为常数函数时, ![]() ;②当
;②当![]() 为增函数时,
为增函数时, ![]() ,即
,即![]() 对任意
对任意![]() 都成立,求二次函数最大值即得解.
都成立,求二次函数最大值即得解.
试题解析:
(1)由![]() ,
,
于是,根据题意设有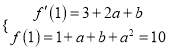 ,
,
解得![]() 或
或![]() ,
,
当![]() 时,所以函数
时,所以函数![]() ,所以函数有极值点;
,所以函数有极值点;
当![]() 时,所以函数
时,所以函数![]() ,所以无极值点,
,所以无极值点,
所以![]() .
.
(2)由题意知![]() 对任意的
对任意的![]() 都成立,
都成立,
所以![]() 对任意的
对任意的![]() 都成立,
都成立,
因为![]() ,所以
,所以![]() 在
在![]() 上为单调增函数或为常数函数,
上为单调增函数或为常数函数,
①当![]() 为常数函数时,
为常数函数时, ![]() ;
;
②当![]() 为增函数时,
为增函数时, ![]() ,
,
即![]() 对任意
对任意![]() 都成立,
都成立,
又![]() ,所以
,所以![]() 时,
时, ![]() ,所以
,所以![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
