Question

【题目】已知等差数列的首项，公差．且、、分别是等比数列的第2、3、4项．

(1)求数列与的通项公式；

(2)设数列满足，求的值（结果保留指数形式）．

Answer 1

【答案】(1) .；. .

(2).

【解析】分析：（1）由题意可得，即，解出即可得，进而得到；

（2）利用错位相减法与等比数列的前n项和公式即可得出.

详解：（1）由题意知等差数列中，且、、成等比，

，

即，又，解得

所以数列的通项公式为

.

再由题意得等比数列中，，，

设等比数列公比为，则，

数列的通项公式为.

()

（2）由（1）得，，，，

设数列的前项的和为，

.

..........① 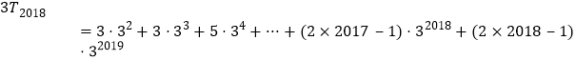..........②

①-②得

所以的值为.

（2）解法2：由（1）得，，，，

设，数列的前项的和为，则

..........①

则..........②

①-②得

，则

故

（2）解法3：由（1）得，，，，

.

设数列的前项的和为，

所以的值为.