题目内容
【题目】在直角坐标系中(![]() 为坐标原点),已知两点
为坐标原点),已知两点![]() ,
,![]() ,且三角形
,且三角形![]() 的内切圆为圆
的内切圆为圆![]() ,从圆
,从圆![]() 外一点
外一点![]() 向圆引切线
向圆引切线![]() ,
,![]() 为切点。
为切点。
(1)求圆![]() 的标准方程.
的标准方程.
(2)已知点![]() ,且
,且![]() ,试判断点
,试判断点![]() 是否总在某一定直线
是否总在某一定直线![]() 上,若是,求出直线
上,若是,求出直线![]() 的方程;若不是,请说明理由.
的方程;若不是,请说明理由.
(3)已知点![]() 在圆
在圆![]() 上运动,求
上运动,求![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1) ![]() .
.
(2) ![]() 在定直线
在定直线![]() 上.
上.
(3) 最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】分析:(![]() )由题意结合几何关系可得圆的半径
)由题意结合几何关系可得圆的半径![]() ,圆心坐标为
,圆心坐标为![]() ,则圆
,则圆![]() 的标准方程为
的标准方程为![]() .
.
(![]() )由题意结合
)由题意结合![]() 可得
可得![]() ,则
,则![]() 在定直线
在定直线![]() 上,
上,
(![]() )设
)设![]() ,由题意可得
,由题意可得![]()
![]() ,结合几何意义可知最大值为
,结合几何意义可知最大值为![]() ,最小值为
,最小值为![]() .
.
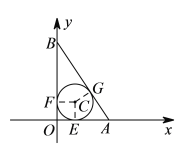
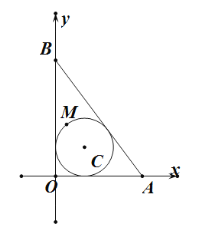
详解:(![]() )设圆
)设圆![]() 与
与![]() ,
,![]() ,
,![]() 的切点为
的切点为![]() 、
、![]() 、
、![]() ,连结
,连结![]() 、
、![]() 、
、![]() ,
,
显然有四边形![]() 为正方形,
为正方形,
设圆![]() 半径为
半径为![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
(![]() )
)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
化简有![]() ,
,
即![]() 满足
满足![]() ,
,
∴![]() 在定直线
在定直线![]() 上,
上,
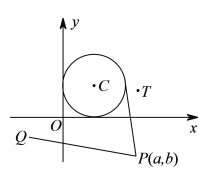
(![]() )设
)设![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
由几何意义可知![]() 表示
表示![]() 到点
到点![]() 距离平方,
距离平方,
点![]() 在圆
在圆![]() 内
内![]() 最大值为
最大值为![]() ,
,
最小值为![]() .
.

练习册系列答案
相关题目