题目内容
10.已知$f(x)=ax-lnx,x∈(0,e],g(x)=\frac{lnx}{x}$,其中e是自然常数,a∈R(Ⅰ)讨论a=1时,函数f(x)的单调性、极值;
(Ⅱ)求证:在(Ⅰ)的条件下,f(x)>g(x)+$\frac{1}{2}$.
分析 (1)当a=1时,求函数的定义域,然后利用导数求函数的极值和单调性.
(2)利用(1)的结论,求函数f(x)的最小值以及g(x)的最大值,利用它们之间的关系证明不等式.
解答 解:(1)a=1时,因为f(x)=x-lnx,f′(x)=1-$\frac{1}{x}$,
∴当0<x<1时,f′(x)<0,此时函数f(x)单调递减.
当1<x≤e时,f′(x)>0,此时函数f(x)单调递增.
所以函数f(x)的极小值为f(1)=1.
(2)因为函数f(x)的极小值为1,即函数f(x)在(0,e]上的最小值为1.
又g′(x)=$\frac{1-lnx}{{x}^{2}}$,所以当0<x<e时,g′(x)>0,此时g(x)单调递增.
所以g(x)的最大值为g(e)=$\frac{1}{e}$,
所以f(x)min-g(x)max>$\frac{1}{2}$,
所以在(1)的条件下,f(x)>g(x)+$\frac{1}{2}$.
点评 本题主要考查利用函数的单调性研究函数的单调性问题,考查函数的极值问题,本题属于中档题..

练习册系列答案
相关题目
18.曲线y=xex+2x-1在点(0,-1)处的切线方程为( )
| A. | y=3x-1 | B. | y=-3x-1 | C. | y=3x+1 | D. | y=-2x-1 |
15.下列命题中的假命题是( )
| A. | ?x∈R,lgx=0 | B. | ?x∈R,tanx=0 | C. | ?x∈R,2x>0 | D. | ?x∈R,x2>0 |
2.若向量$\overrightarrow{a}$•$\overrightarrow{b}$=-2,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
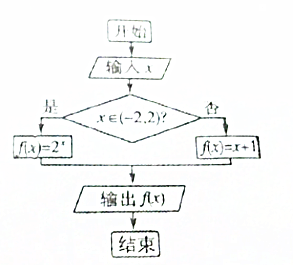 阅读如图的程序框图,若输出的函数值f(x)为4,则输入的自变量x的值为3.
阅读如图的程序框图,若输出的函数值f(x)为4,则输入的自变量x的值为3.