题目内容
2.若向量$\overrightarrow{a}$•$\overrightarrow{b}$=-2,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
分析 根据平面向量的数量积公式求向量的夹角.
解答 解:由已知向量$\overrightarrow{a}$•$\overrightarrow{b}$=-2,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的余弦值为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-2}{4}=-\frac{1}{2}$,由向量的夹角范围是[0,π],
所以向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{2π}{3}$;
故选:A.
点评 本题考查了利用平面向量的数量积公式求向量的夹角;熟记公式是关键.

练习册系列答案
相关题目
12.若函数f(x)=|ax+x2-xlna-m|-3(a>0且a≠1)有两个零点,则m的取值范围( )
| A. | (-2,4) | B. | (-4,2) | C. | (-1,3) | D. | (-3,1) |
7.计算:$\frac{1-co{s}^{2}10°}{cos80°•\sqrt{1-cos20°}}$=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
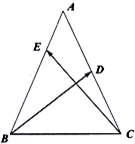 如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.
如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.